
【题目】如图,二次函数![]() 的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.
的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.

(1)求二次函数的解析式;
(2)若抛物线的顶点为D,点E在抛物线上,且与点C关于抛物线的对称轴对称,直线AE交对称轴于点F,试判断四边形CDEF的形状,并说明理由;
(3)若点M在x轴上,点P在抛物线上,是否存在以点A,E,M,P为顶点且以AE为一边的平行四边形?若存在,请求出所有满足要求的点P的坐标;若不存在,请说明理由.
【答案】(1)y=x22x3.(2)四边形EFCD是正方形,理由见解析;P点坐标为(1+![]() ,3)或(1
,3)或(1![]() ,3)或(0,3)
,3)或(0,3)
【解析】
(1)根据抛物线的对称轴为直线x=1得![]() ,求出b,再根据C(0,-3)求出c=-3即可;
,求出b,再根据C(0,-3)求出c=-3即可;
(2)结论四边形EFCD是正方形.如图1中,连接CE与DF交于点K.求出E、F、D、C四点坐标,只要证明DF⊥CE,DF=CE,KC=KE,KF=KD即可证明.
(3)如图2中,存在以A,E,M,P为顶点且以AE为一边的平行四边形.根据点P的纵坐标为3或3,即可解决问题.
(1)∵二次函数![]() 的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.
的图象与x轴相较于A.B两点,与y轴相交于点C(0,-3),抛物线的对称轴为直线x=1.
∴![]()
∴b=-2,
∵C(0,-3)
∴c=-3.
∴抛物线的解析式为y=x22x3.
(2)结论:四边形EFCD是正方形.
理由:如图1中,连接CE与DF交于点K.

∵y=(x1)24,
∴顶点D(1,4),
∵C、E关于对称轴对称,C(0,3),
∴E(2,3),
∵A(1,0),
设直线AE的解析式为y=kx+b,则
![]() ,解得
,解得![]() ,
,
∴直线AE的解析式为y=x1.
∴F(1,2),
∴CK=EK=1,FK=DK=1,
∴四边形EFCD是平行四边形,
又∵CE⊥DF,CE=DF,
∴四边形EFCD是正方形.
(3)如图2中,存在以A,E,M,P为顶点且以AE为一边的平行四边形.

由题意点P的纵坐标为3或3,
当y=3时,x22x3=3,解得x=1±![]() ,
,
可得P1(1+![]() ,2),P2(1
,2),P2(1![]() ,
,
当y=2时,x=0,可得P3(0,3),
综上所述当P点坐标为(1+![]() ,3)或(1
,3)或(1![]() ,3)或(0,3)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.
,3)或(0,3)时,存在以A,E,M,P为顶点且以AE为一边的平行四边形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
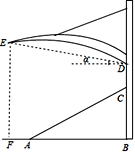
求:(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
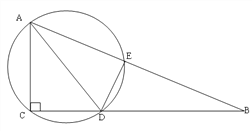
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE。
(1)求证:AC=AE;
(2)求△ACD外接圆的直径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2m+1)x+m2+m=0.
(1)求证:该一元二次方程总有两个不相等的实数根;
(2)若该方程的两根x1、x2是某个等腰三角形的两边长,且该三角形的周长为10,试求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图等腰三角形的顶角![]() =45°,以AB为直径的半圆O与BC,AC相较于点D,E两点,则弧AE所对的圆心角的度数为( )
=45°,以AB为直径的半圆O与BC,AC相较于点D,E两点,则弧AE所对的圆心角的度数为( )
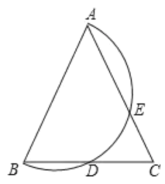
A.40°B.50°
C.90°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
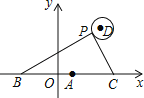
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小区为了促进生活垃圾的分类处理,将生活垃圾分为厨余、可回收和其他三类,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若小明将一袋分好类的生活垃圾随机投入一类垃圾箱,请画树状图或列表求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共100吨生活垃圾,数据统计如下表(单位:吨):
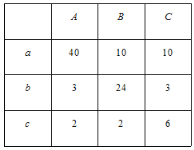
试估计该小区居民“厨余垃圾”投放正确的概率约是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣4x﹣5经过点A(﹣1,0)、B(5,0)
(1)当0<x<5时,y的取值范围为 ;
(2)点P为抛物线上一点,若△PAB的面积S△PAB=21,请求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com