
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
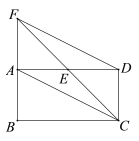
(1)判断四边形ACDF的形状;
(2)当BC=2CD时,求证:CF平分∠BCD.
【答案】(1)四边形ACDF是平行四边形;(2)见解析.
【解析】
(1)利用矩形的性质,即可判定△FAE≌△CDE,即可得到CD=FA,再根据CD∥AF,即可得出四边形ACDF是平行四边形;
(2)先判定ACDF是平行四边形,可得FB=BC,再根据∠BCF=∠DCF=45°,即可得到答案.
解:(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠FAE=∠CDE,
∵E是AD的中点,
∴AE=DE,
又∵∠FEA=∠CED,
∴△FAE≌△CDE,
∴CD=FA,
又∵CD∥AF,
∴四边形ACDF是平行四边形;
(2)证明:∵BC=2CD,ACDF是平行四边形,
∴FB=BC,
∴∠BCF=45°,
∴∠DCF=45°,
∴CF平分∠BCD.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3BC,以点A为圆心,AD为半径画弧交AB于点E连接CE,作线段CE的中垂线交AB于点F,连接CF,则sin∠CFB=_____.
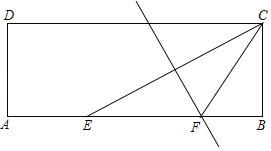
查看答案和解析>>
科目:初中数学 来源: 题型:
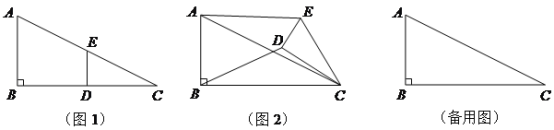
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=ax2-(2a-1)x+a-1(a≠0),有下列结论:①其图象与x轴一定相交;②若a<0,函数在x>1时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《人民日报》点赞湖北宜昌“智慧停车平台”.作为“全国智慧城市”试点,我市通过“互联网”、“大数据”等新科技,打造“智慧停车平台”,着力化解城市“停车难”问题.市内某智慧公共停车场的收费标准是:停车不超过![]() 分钟,不收费;超过
分钟,不收费;超过![]() 分钟,不超过
分钟,不超过![]() 分钟,计
分钟,计![]() 小时,收费
小时,收费![]() 元;超过
元;超过![]() 小时后,超过
小时后,超过![]() 小时的部分按每小时
小时的部分按每小时![]() 元收费(不足
元收费(不足![]() 小时,按
小时,按![]() 小时计).
小时计).
(1)填空:若市民张先生某次在该停车场停车![]() 小时
小时![]() 分钟,应交停车费________元.若李先生也在该停、车场停车,支付停车费
分钟,应交停车费________元.若李先生也在该停、车场停车,支付停车费![]() 元,则停车场按________小时(填整数)计时收费.
元,则停车场按________小时(填整数)计时收费.
(2)当![]() 取整数且
取整数且![]() 时,求该停车场停车费
时,求该停车场停车费![]() (单位:元)关于停车计时
(单位:元)关于停车计时![]() (单位:小时)的函数解析式.
(单位:小时)的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开发了“书画、器乐、戏曲、棋类”四大类兴趣课程.为了解全校学生对每类课程的选择情况,随机抽取了若干名学生进行调查(每人必选且只能选一类),先将调查结果绘制成如下两幅不完整的统计图:
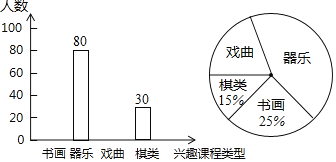
(1)本次随机调查了多少名学生?
(2)补全条形统计图中“书画”、“戏曲”的空缺部分;
(3)若该校共有![]() 名学生,请估计全校学生选择“戏曲”类的人数;
名学生,请估计全校学生选择“戏曲”类的人数;
(4)学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”,用树形图或列表法求处恰好抽到“器乐”和“戏曲”类的概率.(书画、器乐、戏曲、棋类可分别用字幕![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.
I.请问1辆大货车和1辆小货车一次可以分别运货多少吨;
Ⅱ.目前有46.4吨货物需要运输,货运公司拟安排大小货车共10辆,全部货物一次运完.其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com