
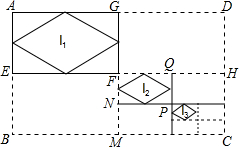
 如图,已知矩形ABCD的边长分别为a,b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形In,则In的面积是($\frac{1}{2}$)2n+1ab.
如图,已知矩形ABCD的边长分别为a,b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形In,则In的面积是($\frac{1}{2}$)2n+1ab. 分析 利用菱形的面积为两对角线乘积的一半,得到菱形I1 的面积,同理可得菱形I2的面积,根据规律可得菱形In的面积.
解答 解:由题意得:菱形I1 的面积为:$\frac{1}{2}$×AG×AE=$\frac{1}{2}$×$\frac{1}{2}a×\frac{1}{2}b$=($\frac{1}{2}$)3•ab;
菱形I2的面积为:$\frac{1}{2}$×FQ×FN=$\frac{1}{2}$×($\frac{1}{2}$×$\frac{1}{2}a$)×($\frac{1}{2}×\frac{1}{2}$b)=($\frac{1}{2}$)5•ab;
…,
∴菱形In的面积为:($\frac{1}{2}$)2n+1ab,
故答案为:($\frac{1}{2}$)2n+1ab.
点评 本题主要考查了菱形面积的计算和规律的归纳,利用菱形的面积为两对角线乘积的一半,是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
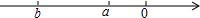 已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )| A. | b<a<-a<-b | B. | b<a<-b<-a | C. | -b<a<-a<b | D. | a<b<-b<-a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
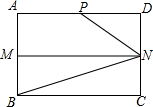 如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,网格图中每一小格的边长都相等.
如图,网格图中每一小格的边长都相等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
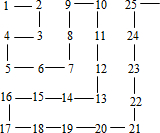 将自然数从1开始,按如图所表示的规律排列,规定图中第m行、第n列的位置记作(m,n),如自然数8的位置是(2,3),则自然数179的位置记作(10,14).
将自然数从1开始,按如图所表示的规律排列,规定图中第m行、第n列的位置记作(m,n),如自然数8的位置是(2,3),则自然数179的位置记作(10,14).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.16×1012 | B. | 4.16×1013 | C. | 0.416×1012 | D. | 416×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com