
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��Ե�M��0��3��ΪԲ�ġ�5Ϊ�뾶��Բ��x�ύ�ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C��D����C�ڵ�D���Ϸ���������B��C����������ߵĶ���E�ڵڶ�����.
(1)�����A��B����������.
(2)�����������ĶԳ�������M����ʱ, ���ʱ�����ߵĽ���ʽ.
(3)������AE��AC��CE����![]() �������E����������ֱ��BC���Ƿ���ڵ�P��ʹ���Ե�B��M��
�������E����������ֱ��BC���Ƿ���ڵ�P��ʹ���Ե�B��M��
PΪ����������κ���ACE���ƣ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵������.
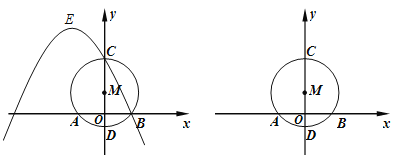
���𰸡�(1)��A(��4,0)��B(4,0)��(2)��![]() ��(3)��E
��(3)��E![]() ��P
��P![]() .
.
��������
���������(1)������AM����������ó�AM=5��OM=3����OA=0B=4����������ꣻ(2)�������������ʽ�����������c=8������B����������ҳ�b��a�Ĺ�ϵʽ�����ֱ�ߵĶԳ���������ߵ����ʵó��Գ���Ϊx=��5�����a��b��ֵ��(3)��������ACO����CAE������ֵ�ó���������ȣ����ݵ�A�ڶԳ����ϣ���ɵó��ԶԳ���Ϊֱ��x=��4�����a��ֵ��Ȼ�������������.
���������(1)������M A��������ã�AM=5��OM=3����OA=4��ͬ����OB=4��
����A����B������ֱ��ǣ�-4��0������4��0��
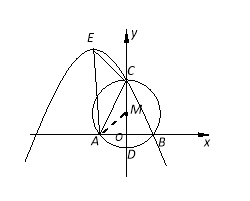
��2���辭��B��C����������߽���ʽΪy=ax2+bx+c��a��0����
��c=8,0=16a+4b+8����b=-4a-2�� ��ʱ��y=ax2+��-4a-2��x+8��a��0����
���ĶԳ�����ֱ�ߣ�x=![]() =
=![]() ��
��
���������ߵĶ���E�ڵڶ������Ҹ������ߵĶԳ�������M���У� ��![]() =-5����a=
=-5����a=![]() ��b=
��b=![]() ��
��
�������ߵĽ���ʽΪ![]()
(3)������Rt��AOC�� tan��ACO=![]() ����tan��CAE=
����tan��CAE=![]()
���CAE=��ACO������AE��CO������A�������ߵĶԳ�����
����y=ax2+��-4a-2��x+8����![]() ����a=
����a=![]() ����
����![]()
![]()
��E![]()
����ֱ��BC�ϴ��ڵ�P��ʹ���Ե�B��M��PΪ����������κ���ACE���ƣ���P������Ϊ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¿�������֤�����⡰�κ�ż������4�ı������Ǽ�����ķ���Ϊ��������
A. 3 B. 4 C. 8 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��2cm/s���ٶ���ͼ1��ʾ�ı߿��B��C��D��E��F��A��·���˶����ǡ�ABP�����Ϊt��cm2����y���˶�ʱ��t��s���Ĺ�ϵ��ͼ2��ʾ��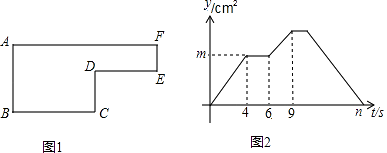
��AB=6cm����ش��������⣺
��1����ͼ1��BC��CD�ij����߿���Χ��ͼ�ε������
��2����ͼ2��m��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����õ�ʽ���ʽ��еı��Σ�����ȷ���ǣ� ��
A.���a=b����ôa��c=b��c
B.���a=b����ôa+c=b+c
C.���a=b����ôac=bc
D.���ac=bc����ôa=b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. 2a2a3=2a6 B. ��3ab��2=6a2b2 C. 2abc+ab=2 D. 3a2b+ba2=4a2b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε����߷ֱ�Ϊ5��10��������ߵij����ܵ��ڣ�������
A.3B.5C.9D.15
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com