
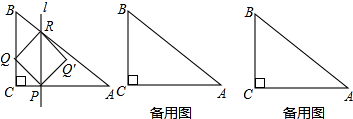
分析 (1)根据Q′是AB的中点,证得D是AC的中点,然后根据对折的性质得出PC的长;根据三角形中位线的性质即可求得结论;
(2)①过Q′作QD⊥AC,由于△PQR与△PQ′R关于直线l对称,a=b,得出PC=PD=a,AD=8-2a,然后解直角三角函数即可求得;
②△PQ′R与△PAR重叠部分有两种情况分别讨论求得.
解答 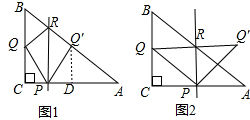 解:(1)b=2,等腰三角形;
解:(1)b=2,等腰三角形;
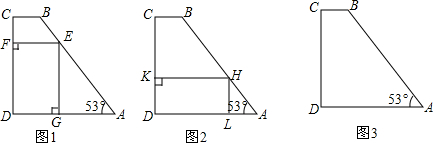
如图1,过Q′作QD⊥AC,
∵Q′是AB的中点,Q′D∥BC,
∴D是AC的中点,
∴CD=$\frac{1}{2}$AC=4,
根据对折的性质:PC=PD=$\frac{1}{2}$CD=2;
如图2,∵a=3,b=4,
∴Q、P分别是BC、AC的中点,
∵PR⊥AC,
∴PR∥BC,
∴R是AB的中点,
∴QR∥AC,
∴QR⊥PR,
∴Q、R、Q′在一条直线上,
∴△PQR与△PQ′R组合而成的轴对称图形的形状是等腰三角形;
故答案是:2;等腰三角形;
(2)①过Q′作QD⊥AC,如图1,
∵△PQR与△PQ′R关于直线l对称,a=b,
∴PC=PD=a,
∴AD=8-2a,
∴tan∠A=$\frac{Q′D}{AD}$=$\frac{BC}{AC}$,
即$\frac{a}{8-2a}$=$\frac{6}{8}$,
解得:a=$\frac{12}{5}$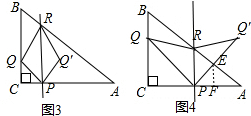 ②(i)当0≤a≤$\frac{12}{5}$时,重叠部分为△PQ′R,如图3,
②(i)当0≤a≤$\frac{12}{5}$时,重叠部分为△PQ′R,如图3,
∵tan∠A=$\frac{RP}{AP}$=$\frac{BC}{AC}$,
∴$\frac{RP}{8-a}$=$\frac{6}{8}$,即RP=$\frac{3}{4}$(8-a),
∴S=$\frac{1}{2}$$\frac{3}{4}$(8-a)•a,
即S=-$\frac{3}{8}$a2+3a (0≤a≤$\frac{12}{5}$)
(ii)当$\frac{12}{5}$<a≤6时,重叠部分为△PER,如图4,
∵∠C=90°,a=b,
∴∠QPC=45°,
∴∠Q′PA=45°,
∴PF=EF,
设EF=m,则PF=m,AF=$\frac{4}{3}$m,
又∵CP+PF+AF=8,
∴a+m+$\frac{4}{3}$m=8,解得:m=$\frac{3}{7}$(8-a),
∴S=$\frac{1}{2}$×$\frac{3}{4}$(8-a)•$\frac{3}{7}$(8-a),
即 S=$\frac{9}{56}$(8-a)2 ($\frac{12}{5}$<a≤6).
综上所述,S=$\left\{\begin{array}{l}{-\frac{3}{8}{a}^{2}+3a(0≤a≤\frac{12}{5})}\\{\frac{9}{56}(8-a)^{2}(\frac{12}{5}<a≤6)}\end{array}\right.$.
点评 此题考查了对折的性质、菱形的判定和性质、勾股定理、等腰三角形的判定、直角三角形的性质以及三角函数等知识.此题综合性很强,难度很大,注意辅助线的作法,注意数形结合思想的应用.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
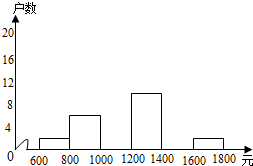 某中学组织同学们进行新农村社会调查,小文负责了解他所居住村庄316户村民的家庭月收入情况.他从中随机调查了40户村民家庭月收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
某中学组织同学们进行新农村社会调查,小文负责了解他所居住村庄316户村民的家庭月收入情况.他从中随机调查了40户村民家庭月收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.| 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | 18 | 45% |
| 1200≤x<1400 | 9 | 22.5% |
| 1400≤x<1600 | 3 | 7.5% |
| 1600≤x<1800 | 2 | 5% |
| 合计 | 40 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 行驶时间x(时) | 0 | 1 | 2 | 3 | 4 |
| 余油量y(升) | 150 | 120 | 90 | 60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.23×106 | B. | 2.2×104 | C. | 22.8×104 | D. | 2.3×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com