
����Ŀ����һ��������ֽƬ�����ĸ���С����״һ����С�����Σ���ͼ��ʾ������Ϊ��һ�β�����Ȼ�����е�һƬ�ְ�ͬ���ķ���������СƬ����Ϊ�ڶ��β��������ѭ��������ȥ���뽫�±��п�ȱ��������д���������������������⣺
�������� | 1 | 2 | 3 | 4 | �� |
������� | 4 | 7 | �� �� | �� �� | �� |
��1�������100�Σ����ܵõ��� ���������Σ�
��2�������n�ι��ܵõ�bn�������Σ����ú���n��bn�ĵ�ʽ��ʾ����֮���������ϵ�� ����
��3����ԭ�����εı߳�Ϊ1����an��ʾ��n�������������εı߳������ú�n��ʽ�ӱ�ʾan�� ����
��4���Բ���a1+a2+a3+a4+��+an��1+an��ԭ�����α߳���������ϵ�����õ�ʽд�������ϵ�� ����

���𰸡���1��301����2��bn=3n+1����3��![]() ����4��1��
����4��1��![]() ��
��
�������������������1���۲�ͼ�μ�������ÿ���һ���ͻ�����3��С�����Σ��ݴ�������ɣ�
��2�����ݵõ��Ĺ��ɵõ�ͨ�ʽ��Ȼ�������ֵ���ɣ�
��3������ÿ�ν��߳�һ��Ϊ�����ɵõ��𰸣�
��4�����÷��ֵĹ��ɣ�������ֵ������ô𰸣�
�⣺�۲�ͼ��֪������һ�Σ���4��С�����Σ�
��������7��С�����Σ�
��������10��С�����Σ�
���Ĵ���13��С�����Σ�
���ɣ�ÿ���һ���ͻ�����3��С�����Σ�
�ʵ�n������4+3��n��1��=3n+1����
��1����n=100��3n+1=3��100=301��
��2����n�ι��ܵõ�bn�������Σ����ú���n��bn�ĵ�ʽ��ʾ����֮���������ϵΪbn=3n+1��
��3����һ�������������εı߳�Ϊ![]() ��
��
�ڶ��������������εı߳�Ϊ![]() ��
��
�����������������εı߳�Ϊ![]() ��
��
��
��n�������������εı߳�an=![]() ��
��
��4��a1+a2+a3+a4+��+an��1+an=![]() +
+![]() +
+![]() +��+
+��+![]() =1��
=1��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ֽ��ÿ��С�����εı߳���Ϊ1.�߶�AB�������˵���С�����εĶ����ϡ�
(1)��ͼ�л�һ����ABΪ���ĵ�����������ABC����C��С�����εĶ����ϣ���tan��B=3��
(2)��ͼ�л�һ����ABΪ�ĵ�����������ABD,��D��С�����ε������,����ABD�����������.����CD,��ֱ��д���߶�CD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ�֪���κ�һ�����������е������ֶ��壺a�Dz�Ϊ��1�������������ǰ�![]() ��Ϊ������a�ĺ͵�����������������壬����������⣺
��Ϊ������a�ĺ͵�����������������壬����������⣺
��1����������2�ĺ͵�����
��2������������5�ĺ͵�����
��3����֪a1��1��a2��a1�ĺ͵�����a3��a2�ĺ͵�����a4��a3�ĺ͵������������������ƣ���a10��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���α�����һ̽�������ͼ1���мס������������Σ����������ڽǷֱ�Ϊ10�㣬20�㣬150�㣻���������ڽǷֱ�Ϊ80�㣬25�㣬75�㣮���ܰ�ÿһ�������ηֳ����������������𣿻�һ���������ÿ�����������ζ��ǵĶ�����
��1��С����Ҫ����ͼ1�м�ͼ�ķָ��ߣ������������ͼ1����ͼ�ķָ��ߣ�
��2��С����һ��̽�����֣��ܽ�һ������Ϊ108��ĵ��������ηֳ��������������Σ�����ͼ2�������ֲ�ͬ�ķ��������ָ��ߣ�����עÿ�����������ζ��ǵĶ������������ַ����ֵõ������γ�3��ȫ�������Σ�����Ϊͬһ�ַ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ĵ�A��B��C��D��
��1��������AD��������д��ͼ���̣�
��2��������P��ʹPA+PB+PC+PD��ֵ��С��������д��ͼ���̣�
��3���ڣ�2���������£���S��ABP��2��S��ADP��6��S��BCP��1.5����S��DCP���� ����
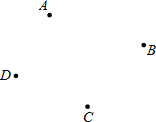
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��150����OCΪ��AOB�ڲ���һ�����ߣ���BOC��60����
��1����ͼ1����OEƽ�֡�AOB��ODΪ��BOC�ڲ���һ�����ߣ���COD��![]() ��BOD�����DOE�Ķ�����
��BOD�����DOE�Ķ�����
��2����ͼ2��������OE����O���OA��ʼ��15��/����ٶ�˳ʱ����ת��OB������OF����O���OB��ʼ��5������ٶ���ʱ����ת��OA�������˶�ʱ��Ϊt�룬����EOC����FOCʱ����t��ֵ��
��3��������OM����O���OA��ʼ��15������ٶ���ʱ����ת��OB����������ת�����У�ONƽ�֡�AOM������2��BONһ��BOM��ijʱ������Ƿ�Ϊ��ֵ�������ǣ���˵�����ɣ������벹ȫͼ�Σ���������ֵ��д��t���ڵ�ʱ��Σ��������еĽǾ�Ϊ����0����С��180���Ľǣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й�����Ѹ�ͷ�չ�������ǵij��д�������ı�ݣ���ͼ1����ij������ƶ�����ͷ���ݽ���һ���֣�����OBA��һ�������Գ���������ˮƽ��OC�������ߵ�һ���֣���A��B�dz�ͷ�����ֵ���ߵ����͵㣬AC��BD�����㵽����ײ��ľ��룬OD=1.5�ף�BD=1.5�ף�AC=3�ף�����������ѧ�ĺ���֪ʶ����������⣮
��1��Ϊ�˷����о����⣬��Ҫ������OBA�Ƶ�O��תת��Ϊ������Ϥ�ĺ����������������ķ����ڣ���������ת����ͼ��IJ�ͼ����ͼ�б����O��A��B��C��D��Ӧ��λ�ã������������ĺ����Ľ���ʽ��
��2����ͼ2����ʻԱ���ΰ�װ��ˮƽ��OC��һ��P����ʵ���������PA+PB��Сʱ����ʻԱ��ʻʱ��Ұ��ѣ�Ϊ�˴ﵽ�����Ұ����OP�ij���
��3����ʻԱͷ���������ֵĸ߶�����Ϊ0.3�ײŸе�ѹ�֣�һ����ʻԱ����ʱͷ��������ľ���Ϊ1�ף��ڣ�2��������£������������������ʱ���Ÿе����ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С�������ɽ���棬�����³�������ɽ�³��ĵ��侭����A�����Bʱ����������200 m���³���ʻ��·����ˮƽ�н��Ϧ�=16�������³������ɵ�B�����Dʱ�������߹���200 m���³��ɵ�B����D����ʻ·����ˮƽ�н��Ϧ�=42�������³��ӵ�A����D��ֱ�����ľ��룮������������������ο����ݣ�sin16���0.27��cos16���0.77��sin42���0.66��cos42���0.74��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ���ʾ��
���ʾ��![]() ��
��![]() ���ʾ��
���ʾ��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ���߶�
���߶�![]() ��һ�㣬
��һ�㣬![]() ��
�� ![]() �ֱ��
�ֱ��![]() ��
��![]() ��������1����λ/�롢3����λ/����ٶ���ֱ��
��������1����λ/�롢3����λ/����ٶ���ֱ��![]() �����˶���
�����˶���![]() ���߶�
���߶�![]() ���˶���
���˶���![]() ���߶�
���߶�![]() ���˶���
���˶���
��1�����߶�![]() �ij��ȣ�
�ij��ȣ�
��2�����˶�4���![]() ���3����λ����
���3����λ����![]() �������ϵ�λ�ã�
�������ϵ�λ�ã�
��3�������˶������У�����![]() ����˵����
����˵����![]() �������ϵ�λ�ã�
�������ϵ�λ�ã�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com