
【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.

① ________;②________;③________;④________.
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:_________________________;
(3)利用(2)的结论计算99992+2×9999×1+1的值.
【答案】(1)①![]() ,②2ab,③
,②2ab,③![]() ,④
,④![]() ;(2)
;(2)![]() ;(3)100000000.
;(3)100000000.
【解析】试题分析:(1)①正方形边长为a,则它的面积为a2;②一个矩形的长为a,宽为b,矩形的面积为ab,再乘以2得到2个矩形的面积为2ab;③正方形边长为b,则它的面积为b2;④正方形的边长为a+b,所以正方形的面积为(a+b)2;(2)第四个图形的面积为前面三个图形面积之和,即a2+2ab+b2=(a+b)2;(3)99992+2×9999×1+1符合a2+2ab+b2形式,故直接套用公式99992+2×9999×1+1=(9999+1)2=100000000.
试题解析:
(1)①a2;②2ab;③b2;④(a+b)2;
(2)a2+2ab+b2=(a+b)2;
(3)解:99992+2×9999×1+1=(9999+1)2=100000000.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】解方程:(1)2(1-x)2-8=0 (2)2x2![]() x-1=0 (3)x2-3x+1=0(配方法)
x-1=0 (3)x2-3x+1=0(配方法)
(4)(x+3)(x-1)=5. (5) (x-1)2-5(x-1)+6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图![]() ,在正方形
,在正方形![]() 的内部,作
的内部,作![]() ,根据三角形全等的条件,易得
,根据三角形全等的条件,易得![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,从而得到四边形
,从而得到四边形![]() 是正方形.
是正方形.
类比探究
如图![]() ,在正
,在正![]() 的内部,作
的内部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两相交于
两两相交于![]() ,
, ![]() ,
, ![]() 三点(
三点(![]() ,
, ![]() ,
, ![]() 三点不重合).
三点不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(![]() )
)![]() 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
(![]() )进一步探究发现,图
)进一步探究发现,图![]() 中的
中的![]() 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设![]() ,
, ![]() ,
, ![]() ,请探索
,请探索![]() ,
, ![]() ,
, ![]() 满足的等量关系.
满足的等量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
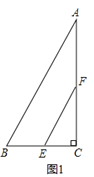
(1)![]() = .
= .
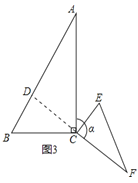
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,求线段BE与线段AF的位置关系和![]() 。
。

(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2![]() ,求旋转角a的度数.
,求旋转角a的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 在同一平面内,过一点有且只有一条直线与已知直线垂直
B. 对顶角相等
C. 两直线平行,同位角相等
D. 同旁内角互补
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com