
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连结AP.
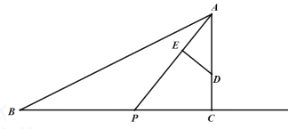
(1)当t=3秒时,求AP的长度(结果保留根号);
(2)当△ABP为等腰三角形时,求t的值;
(3)过点D做DE⊥AP于点E.在点P的运动过程中,当t为何值时,能使DE=CD?
【答案】(1)AP=![]() ;(2)t=
;(2)t=![]() 或16或5;(3)t=5或11.
或16或5;(3)t=5或11.
【解析】
(1)根据t=3求出BP的长度,进而得到CP的长度,根据勾股定理即可得出答案;
(2)分三种情况进行讨论:①若BA=BP②若AB=AP③若PA=PB分别计算即可得出答案;
(3)分情况进行讨论:①若P在C点的左侧②若P在C点的右侧,根据勾股定理即可得出答案.
(1)当t=3时,BP=6,则CP=10
又∵AC=8
∴AP=![]() =
=![]() =
=![]()
(2)∵BC=16,AC=8
∴BA=![]()
①若BA=BP,则 ![]() ;
;
②若AB=AP,则CP=![]() ,BP=32,t=16;
,BP=32,t=16;
③若PA=PB,则BP=AP=2t,CP=16-2t
在直角三角形ACP中,![]()
![]() ,解得:t=5
,解得:t=5
综上所述:t=![]() 或16或5.
或16或5.
(3)分类讨论
∵DE=CD=3,AD=AC-CD=8-3=5
∴AE=4
①若P在C点的左侧,则BP=2t
∴CP=16-2t.
又DE=DC且∠DEP=∠DCP=90°
∴D在∠EPC的角平分线上故PE=PC=16-2t
∴AP=PE+AE=20-2t
则 ![]()
解得t=5
②若P在C点的右侧,则BP=2t
∴CP=2t-16
又DE=DC且∠DEP=∠DCP=90°
∴D在∠EPC的角平分线上故PE=PC=2t-16
∴AP= PE+AE=2t-12
![]()
解得t=11
综上所述:t=5或11.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车,A型自行车售价为2200元/辆,B型自行车售价为1750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80000元购进A型自行车的数量与用64000元购进B型自行车的数量相等.
(1)求A,B两种自行车的进价分别是多少元/辆?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为w元,要求购进B型自行车数量不少于A型自行车数量的2倍,且A型车辆至少30辆,请用含m的代数式表示w,并求获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华有一个容量为8GB (1GB= 1024MB)的U盘,U盘中已经存储了一个视频文件,其余空间都用来存储照片,若每张照片占用的内存容量均相同,图片数量x (张)和剩余可用空间y (MB)的部分关系如表:
图片数量 | 100 | 150 | 200 | 400 | 800 |
剩余可用空间 | 5700 | 5550 | 5400 | 4800 | 3600 |
(1)由上表可知,y与x之间满足___ ___(填“一次”或“二次”或“反比例”)函数的关系,求出y与x之间的关系式.
(2)求出U盘中视频文件的占用内存容量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明(视为小黑点)站在一个高为10米的高台A上,利用旗杆OM顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B.那么小明在荡绳索的过程中离地面的最低点的高度MN是( )

A.2米B.2.2米C.2.5米D.2.7米
查看答案和解析>>
科目:初中数学 来源: 题型:
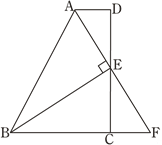
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有2位股东,25名工人,从2006年至2008年,公司每年股东的总利润和每年工人的工资总额如图所示.

(1)填写下表
年份 | 2006年 | 2007年 | 2008年 |
工人的平均工资/元 |
|
|
|
股东的平均工资/元 |
|
|
|
(2)假设在以后的若干年中,每年工人的工资和股东的利润都按图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的10倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 之间的关系是( )
之间的关系是( )

A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组进行户外兴趣活动:测量河中桥墩露出水面部分AB的高度.如图所示,在点C处测得∠BCA=45°.在坡比为i=1:3,高度DE=15米的小山坡顶E处测得桥墩顶部B的仰角为20°,则桥墩露出水面部分AB的高度约为(精确到1米,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)( )

A. 34 B. 48 C. 49 D. 64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com