
【题目】某校数学兴趣小组进行户外兴趣活动:测量河中桥墩露出水面部分AB的高度.如图所示,在点C处测得∠BCA=45°.在坡比为i=1:3,高度DE=15米的小山坡顶E处测得桥墩顶部B的仰角为20°,则桥墩露出水面部分AB的高度约为(精确到1米,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)( )

A. 34 B. 48 C. 49 D. 64
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连结AP.
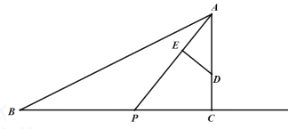
(1)当t=3秒时,求AP的长度(结果保留根号);
(2)当△ABP为等腰三角形时,求t的值;
(3)过点D做DE⊥AP于点E.在点P的运动过程中,当t为何值时,能使DE=CD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,过点B作BD⊥AC于点D,BE平分∠ABD交AC于点E.

(1)求证:CB=CE;
(2)若∠CEB=80°,求∠DBC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边 且BE=CF,AD+EC=AB.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点 A1,A2,A3…在射线ON 上,点B1,B2,B3…在射线OM 上,△A1B1A2,△A2B3A3,△A3B3A4![]() 均为等边三角形,若OA1=2,则△A7B7A8 的边长为____.
均为等边三角形,若OA1=2,则△A7B7A8 的边长为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点,AB为腰,在第三象限作等腰Rt△ABC.

(1)求C点的坐标及△ABC的面积;
(2)如图2,P为y轴负半轴上一个动点,当P点在y轴负半轴上向下运动时,若以P为直角顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求证:OP=DE+2.
(3)已知点F坐标为(-2,-2),当G在y轴的负半轴上沿负方向运动时,请在图3作出等腰Rt△FGH,且始终保持∠GFH=90°,若FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0), 当G在y轴的负半轴上沿负方向运动时,以下结论:①m-n为定值;②m+n为定值,请判断其中哪些结论是正确的,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴和
轴和![]() 轴交于
轴交于![]() ,
,![]() 两点,且与正比例函数
两点,且与正比例函数![]() 的图象交于点
的图象交于点![]() .
.

(1)求![]() 的值;
的值;
(2)求正比例函数的表达式;
(3)点![]() 是一次函数图象上的一点,且
是一次函数图象上的一点,且![]() 的面积是3,求点
的面积是3,求点![]() 的坐标;
的坐标;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的值最小?若存在,求出点
的值最小?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在BC上,且四边形AEFD是平行四边形.
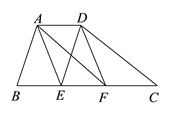
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,求证:四边形AEFD是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com