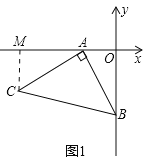
【题目】如图1，OA=2，OB=4,以A点为顶点，AB为腰，在第三象限作等腰Rt△ABC.

(1)求C点的坐标及△ABC的面积；

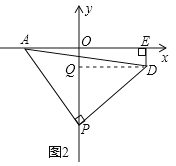
(2)如图2，P为y轴负半轴上一个动点，当P点在y轴负半轴上向下运动时，若以P为直角顶点，PA为腰作等腰Rt△APD，过D作DE⊥x轴于E点，求证：OP=DE+2．

(3)已知点F坐标为（-2，-2），当G在y轴的负半轴上沿负方向运动时，请在图3作出等腰Rt△FGH，且始终保持∠GFH=90°，若FG与y轴负半轴交于点G（0，m），FH与x轴正半轴交于点H（n，0）， 当G在y轴的负半轴上沿负方向运动时，以下结论：①m-n为定值；②m+n为定值,请判断其中哪些结论是正确的，并求出其值.

参考答案：

【答案】（1）①C（-6，-2）；②10；（2）证明见解析；（3）②，m+n=-4.

【解析】

（1）如图1，过C作CM⊥x轴于M点，则可以求出△MAC≌△OBA，可得CM=OA=1，MA=OB=2，故点C的坐标为（-3，-1）；再由勾股定理求出AB、AC的长即可求出△ABC的面积；

（2）如图2，过D作DQ⊥OP于Q点，则DE=OQ，利用三角形全等的判定定理可得△AOP≌△PQD（AAS），进一步可得PQ=OA=2，即OP-DE=2，从而得到结论；

（1）①如图1，过C作CM⊥x轴于M点，

∵∠MAC+∠OAB=90°，∠OAB+∠OBA=90°，

则∠MAC=∠OBA，

在△MAC和△OBA中

，

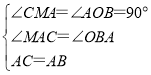∴△MAC≌△OBA（AAS），

∴CM=OA=2，MA=OB=4，

∴OM=OA+AM=2+4=6，

∴点C的坐标为（-6，-2）．

②在Rt△AOB中，AB=AC=，

∴S△ACB=ACAB=10．

（2）证明：如图2，过D作DQ⊥OP于Q点，则DE=OQ

∴OP-DE=OP-OQ=PQ，

∵∠APO+∠QPD=90°，

∠APO+∠OAP=90°，

∴∠QPD=∠OAP，

在△AOP和△PQD中，

，

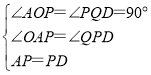∴△AOP≌△PQD（AAS）．

∴PQ=OA=2．

即OP = DE+2．

（3）结论②是正确的，m+n=-4，

如图3，过点F分别作FS⊥x轴于S点，FT⊥y轴于T点，则FS=FT=2，∠FHS=∠HFT=∠FGT，

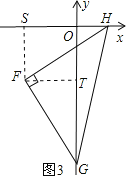
在△FSH和△FTG中，

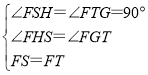
则△FSH≌△FTG（AAS）

则GT=HS，

又∵G（0，m），H（n，0），点F坐标为（-2，-2），

∴OT═OS=2，OG=|m|=-m，OH=n，

∴GT=OG-OT=-m-2，HS=OH+OS=n+2，

则-2-m=n+2，

则m+n=-4．

关闭