
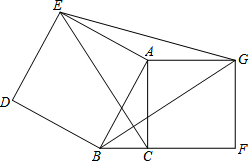
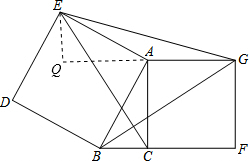
 如图,在△ABC中,∠ACB=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接CE,BG,EG.(正方形的各边都相等,各角均为90°)
如图,在△ABC中,∠ACB=90°,分别以边AB、AC向外作正方形ABDE和正方形ACFG,连接CE,BG,EG.(正方形的各边都相等,各角均为90°)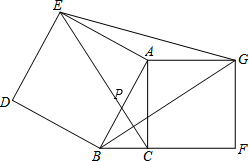
|
| BC |
| AB |
| AB2-AC2 |
| 1 |
| 2 |
| 1 |
| 2 |


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
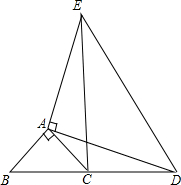 如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.
如图,△ABC和△ADE都是等腰三角形,AB=AC,AD=AE,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.则线段BD与CE有什么关系?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 几何体简称为体,按其形状可分为三类,即柱体、椎体、球体,下列图形中:
几何体简称为体,按其形状可分为三类,即柱体、椎体、球体,下列图形中:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为灰色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.
如图所示,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为灰色瓷砖,其余部分全为白色瓷砖.设纵向每排有n块瓷砖.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com