
 在线段AB上有两点C,D且AD:BD=8:6,AC:CB=2:3,若AB=90cm
在线段AB上有两点C,D且AD:BD=8:6,AC:CB=2:3,若AB=90cm分析 (1)由题意可知AD=$\frac{4}{7}AB$,AC=$\frac{2}{5}$AB,由CD=AD-AC可求得CD与AB之间的数量关系;
(2)由(1)可知:CD=$\frac{6}{35}$AB,最后将AB的长代入计算即可.
解答 解:(1)∵AD:BD=8:6,
∴AD=$\frac{4}{7}AB$.
∵AC:CB=2:3,
∴AC=$\frac{2}{5}$AB.
∵CD=AD-AC,
∴CD=$\frac{4}{7}AB-\frac{2}{5}AB$=$\frac{6}{35}$AB.
(2)CD=$\frac{6}{35}$AB=$\frac{6}{35}×90$=$\frac{108}{7}$.
点评 本题主要考查的是两点间的距离,根据题目所给的比例关系,找出各条线段与AB的数量关系是解题的关键.


科目:初中数学 来源: 题型:解答题
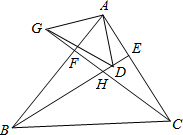 如图,在△ABC中,BE,CF分别是AC,AB边上的高,在BE上截取BD=AC,延长CF至G,使CG=AB,连接AD,AG,GD,试判断△AGD的形状.
如图,在△ABC中,BE,CF分别是AC,AB边上的高,在BE上截取BD=AC,延长CF至G,使CG=AB,连接AD,AG,GD,试判断△AGD的形状.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
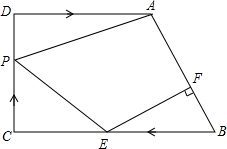 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com