
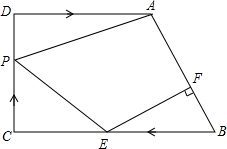
 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)分析 (1)过点A作AM⊥BC,在Rt△ABM中,利用勾股定理可得结果;
(2)由PE∥AB,利用相似三角形的判定定理(AA)可得△PCE∽△AMB,由PC=t,CE=10-2t,BM=2t,利用相似三角形的性质可得t;
(3)首先利用AA定理证得△AMB∽△EFB,由相似三角形的性质可得EF,BF,利用三角形的面积公式求得△CPE,△EFB,△EFB的面积,利用S=S梯形ABCD-S△ADP-S△CPE-S△EFP可得结果;
(4)利用(3)的结果,根据题意可得S=$\frac{5}{9}$S梯形ABCD,解得t,看t是否在0<t<5判断是否存在,根据t得BE,确定点E的位置.
解答 解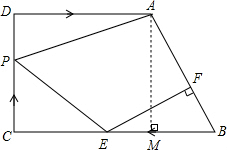 :(1)过点A作AM⊥BC,
:(1)过点A作AM⊥BC,
在Rt△ABM中,AM=CD=6cm,BM=BC-CM=BC-AD=10-8=2cm,
∴AB=$\sqrt{{AM}^{2}{+BM}^{2}}$=$\sqrt{{6}^{2}{+2}^{2}}$=2$\sqrt{10}$(cm);
(2)若PE∥AB,则∠PEC=∠B,
∵∠C=∠AMB=90°,
∴△PCE∽△AMB,
∴$\frac{PC}{AM}=\frac{CE}{MB}$,
∵PC=t×1=t,CE=10-2t,BM=2t,
∴$\frac{t}{6}=\frac{10-2t}{2}$,
解得:t=$\frac{30}{7}$(秒 ),
∴当t=$\frac{30}{7}$秒时,PE∥AB;
(3)∵∠B=∠B,∠AMB=∠EFB,
∴△AMB∽△EFB,
∴$\frac{AM}{EF}=\frac{AB}{EB}$=$\frac{MB}{FB}$,
∴$\frac{6}{EF}=\frac{2\sqrt{10}}{2t}$=$\frac{2}{FB}$,
∴EF=$\frac{3\sqrt{10}}{5}t$,FB=$\frac{\sqrt{10}}{5}t$,
∵S梯形ABCD=$\frac{1}{2}×(8+10)×6$=54,
${S}_{△ADP}=\frac{1}{2}×AD×DP=\frac{1}{2}×8×(6-t)$=24-4t,
${S}_{△CPE}=\frac{1}{2}×CP×CE=\frac{1}{2}t(10-2t)$=-t2+5t,
S△EFB=$\frac{1}{2}×BF×EF$=$\frac{1}{2}×\frac{\sqrt{10}}{5}t×\frac{3\sqrt{10}}{5}t$=$\frac{3}{5}$t2,
∴S=S梯形ABCD-S△ADP-S△CPE-S△EFP=$\frac{1}{2}×(8+10)×6$-(24-4t)-(-t2+5t)-$\frac{3}{5}$t2,
∴S=$\frac{2}{5}$t2-t+30;
(4)存在.
由题意得,$\frac{2}{5}$t2-t+30=$\frac{5}{9}×54$=30,
解得:t1=0,${t}_{2}=\frac{5}{2}$,
∵0<t<5,
∴当t=$\frac{5}{2}$时,使得四边形APEF的面积是梯形ABCD面积的$\frac{5}{9}$,
∴BE=2×$\frac{5}{2}$=5,
即点E是BC的中点.
点评 本题主要考查了相似三角形的性质及判定定理和勾股定理,作出适当的辅助线构建直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:填空题
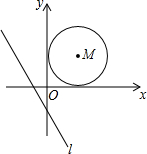 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为2.5或10秒.
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为2.5或10秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
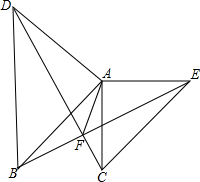 如图,在△ABD中,AD=AB,∠DAB=90°,在△ACE中,AC=AE,∠EAC=90°,CD,BE相交于点F.求证:
如图,在△ABD中,AD=AB,∠DAB=90°,在△ACE中,AC=AE,∠EAC=90°,CD,BE相交于点F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
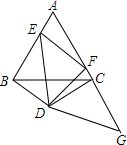 如图,△ABC是边长为4的等边三角形,以BC为底边作一个顶角为120°的等腰三角形△DBC,以D为顶点作∠EDF=60°,使点E,F分别在边AB,边AC上运动,G在AC延长线上且CG=BE,连接EF,GD.
如图,△ABC是边长为4的等边三角形,以BC为底边作一个顶角为120°的等腰三角形△DBC,以D为顶点作∠EDF=60°,使点E,F分别在边AB,边AC上运动,G在AC延长线上且CG=BE,连接EF,GD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
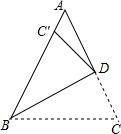 如图,在△ABC中,AB=AC,∠BAC=48°,点D在AC上,将△ABC沿BD折叠,若点C恰好落在AB边上的C′处,则∠AC′D的度数是114°.
如图,在△ABC中,AB=AC,∠BAC=48°,点D在AC上,将△ABC沿BD折叠,若点C恰好落在AB边上的C′处,则∠AC′D的度数是114°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABO的顶点O是平面直角坐标系的原点,∠AOB=90°,BO=3AO,当点A在反比例函数y=-$\frac{2}{x}$(x<0)的图象上移动时,点B也在另一反比例函数y=$\frac{k}{x}$的图象上,试求反比例函数y=$\frac{k}{x}$的解析式.
如图,Rt△ABO的顶点O是平面直角坐标系的原点,∠AOB=90°,BO=3AO,当点A在反比例函数y=-$\frac{2}{x}$(x<0)的图象上移动时,点B也在另一反比例函数y=$\frac{k}{x}$的图象上,试求反比例函数y=$\frac{k}{x}$的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com