
 如图,Rt△ABO的顶点O是平面直角坐标系的原点,∠AOB=90°,BO=3AO,当点A在反比例函数y=-$\frac{2}{x}$(x<0)的图象上移动时,点B也在另一反比例函数y=$\frac{k}{x}$的图象上,试求反比例函数y=$\frac{k}{x}$的解析式.
如图,Rt△ABO的顶点O是平面直角坐标系的原点,∠AOB=90°,BO=3AO,当点A在反比例函数y=-$\frac{2}{x}$(x<0)的图象上移动时,点B也在另一反比例函数y=$\frac{k}{x}$的图象上,试求反比例函数y=$\frac{k}{x}$的解析式. 分析 首先设B点坐标满足的函数解析式是y=$\frac{k}{x}$,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,易得△AOC∽△OBD,然后由相似三角形面积比等于相似比的平方,求得S△AOC:S△BOD=$\frac{1}{9}$,继而求得答案.
解答 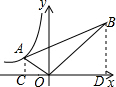 解:设B点坐标满足的函数解析式是y=$\frac{k}{x}$,
解:设B点坐标满足的函数解析式是y=$\frac{k}{x}$,
过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=($\frac{OA}{OB}$)2,
∵BO=3AO,
∴S△AOC:S△BOD=$\frac{1}{9}$,
∵S△AOC=$\frac{1}{2}$OC•AC=$\frac{1}{2}$×2=1,S△BOD=$\frac{1}{2}$OD•BD=$\frac{1}{2}$|k|,
∴k=18,
∴B点坐标满足的函数解析式是y=$\frac{18}{x}$.
点评 此题考查了待定系数法求反比例函数的解析式,相似三角形的判定与性质以及反比例函数的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题
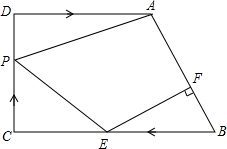 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
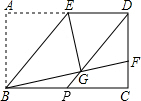 如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.
如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
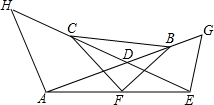 如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.
如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com