
���� ��1�����������е��ٶ���x��/�֣����������г����ٶ�Ϊ3x��/�֣����ݵ�����ϵ�������г���ѧУ������ѧУ���е�����ʱ��20���ӿɵó����̣�������ɣ�
��2����������С��ﳵ���ڼ��õ��ߵ�ʱ��ͣ�Ȼ����42�Ƚϼ��������жϣ�
��� �⣺��1�����������е��ٶ���x��/�֣����������г����ٶ���3x��/�֣�
�������⣬��$\frac{2100}{x}$-$\frac{2100}{3x}$=20��
���x=70��
�����飬x=70��ԭ���̵Ľ⣬
���������е��ٶ���70��/�֣�
��2����Ϊ$\frac{2100}{70}$+$\frac{2100}{3��70}$+1=41���֣���42���֣���
�����������������Ὺʼǰ�ϵ�ѧУ��
���� ���⿼���˷�ʽ���̵�Ӧ�ã�������е��ٶȣ����ݵ�����ϵ�ó������ǽ����Ĺؼ���ע���ʽ����һ��Ҫ���飮


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д� ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Rt��ABO�Ķ���O��ƽ��ֱ������ϵ��ԭ�㣬��AOB=90�㣬BO=3AO������A�ڷ���������y=-$\frac{2}{x}$��x��0����ͼ�����ƶ�ʱ����BҲ����һ����������y=$\frac{k}{x}$��ͼ���ϣ�����������y=$\frac{k}{x}$�Ľ���ʽ��
��ͼ��Rt��ABO�Ķ���O��ƽ��ֱ������ϵ��ԭ�㣬��AOB=90�㣬BO=3AO������A�ڷ���������y=-$\frac{2}{x}$��x��0����ͼ�����ƶ�ʱ����BҲ����һ����������y=$\frac{k}{x}$��ͼ���ϣ�����������y=$\frac{k}{x}$�Ľ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
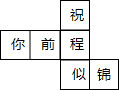 ��ͼ��ˮƽ���õ��������������ֱ��á�ǰ�桢���桢���桢���桢���桢���桱��ʾ����ͼ����һ���������ƽ��չ��ͼ����ͼ�еġ��ơ���ʾ�������ǰ�棬��������ʾ���棬���̡���ʾ���棬���㡱������������森
��ͼ��ˮƽ���õ��������������ֱ��á�ǰ�桢���桢���桢���桢���桢���桱��ʾ����ͼ����һ���������ƽ��չ��ͼ����ͼ�еġ��ơ���ʾ�������ǰ�棬��������ʾ���棬���̡���ʾ���棬���㡱������������森�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
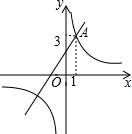 ��ͼ������������$y=\frac{k}{x}$��ͼ��λ�ڵ�һ�������ޣ����е�һ�����ڵ�ͼ����A��1��3�������ڵ��������ڵ�ͼ������һ����ϲ���ĵ�P����ѡ���P������Ϊ��-1��-3����
��ͼ������������$y=\frac{k}{x}$��ͼ��λ�ڵ�һ�������ޣ����е�һ�����ڵ�ͼ����A��1��3�������ڵ��������ڵ�ͼ������һ����ϲ���ĵ�P����ѡ���P������Ϊ��-1��-3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com