
分析 (1)先根据分式混合运算的法则把原式进行化简,再把a、b的值代入进行计算即可;
(2)先把各根式化为最减二次根式,再合并同类项即可;
(3)先把分式方程化为整式方程,再求出x的值,代入公分母进行检验即可;
(4)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=1-$\frac{a-b}{a}$÷$\frac{(a+b)(a-b)}{a(a-b)}$
=1-$\frac{a-b}{a}$•$\frac{a}{a+b}$
=1-$\frac{a-b}{a+b}$
=$\frac{2b}{a+b}$,
当a=-$\frac{1}{2}$,b=1时,原式=$\frac{2×1}{-\frac{1}{2}+1}$=4;
(2)原式=5-$\frac{\sqrt{2}}{6}$+$\sqrt{2}$+1
=6+$\frac{5\sqrt{2}}{6}$;
(3)原方程可化为3-x=2(x-2),
整理得,3x-4=3,解得x=$\frac{7}{3}$,
经检验,x=$\frac{7}{3}$是原分式方程的根;
(4)$\left\{\begin{array}{l}6x+2<4x①\\ \frac{2x-1}{5}<\frac{x+1}{2}②\end{array}\right.$,由①得,x<-1,由②得,x>-7,
故不等式的解集为:-7<x<-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
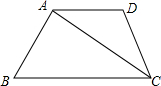 如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cosB=$\frac{5}{13}$,BC=26.求cos∠DAC的值和腰长CD.
如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cosB=$\frac{5}{13}$,BC=26.求cos∠DAC的值和腰长CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com