
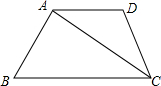
 如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cosB=$\frac{5}{13}$,BC=26.求cos∠DAC的值和腰长CD.
如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cosB=$\frac{5}{13}$,BC=26.求cos∠DAC的值和腰长CD. 分析 解Rt△ABC求出AB,根据勾股定理求出AC,根据平行线性质求出∠DAC=∠ACB,利用余弦函数定义求出cos∠ACB即可得到cos∠DAC的值;过D作DE⊥AC于E,根据等腰三角形的性质求出AE=EC=12,根据cos∠DAC=$\frac{12}{13}$即可求出腰长CD.
解答 解:∵AC⊥AB,
∴∠BAC=90°,
∵在Rt△ABC中,cosB=$\frac{AB}{BC}=\frac{5}{13}$,BC=26,
∴AB=10,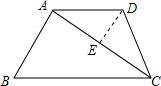 ∴$AC=\sqrt{B{C^2}-A{B^2}}=\sqrt{{{26}^2}-{{10}^2}}=24$.
∴$AC=\sqrt{B{C^2}-A{B^2}}=\sqrt{{{26}^2}-{{10}^2}}=24$.
∵AD∥BC,
∴∠DAC=∠ACB,
∴cos∠DAC=cos∠ACB=$\frac{AC}{BC}=\frac{24}{26}=\frac{12}{13}$;
过点D作DE⊥AC,垂足为E,
∵AD=DC,
∴∠DAC=∠DCE,AE=EC=$\frac{1}{2}$AC=12,
在Rt△CDE中,cos∠DCE=cos∠DAC=$\frac{CE}{DC}=\frac{12}{13}$,
∴DC=$\frac{13EC}{12}$=13.
点评 本题考查了解直角三角形,等腰三角形的性质,勾股定理,平行线的性质,锐角三角函数的定义,能正确解直角三角形是解此题的关键,注意数形结合思想的应用.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:填空题
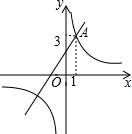 如图,反比例函数$y=\frac{k}{x}$的图象位于第一、三象限,其中第一象限内的图象经过点A(1,3),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为(-1,-3).
如图,反比例函数$y=\frac{k}{x}$的图象位于第一、三象限,其中第一象限内的图象经过点A(1,3),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为(-1,-3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com