
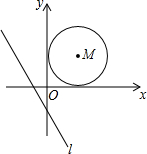 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为2.5或10秒.
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为2.5或10秒. 分析 根据题意确定直线的相对速度,作出直线与圆相切时的图形,求出AM、AE,证明△ADM∽△AEC,△ADM∽△AFG得到成比例线段,求出时间.
解答 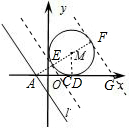 解:∵直线以每秒3个单位的速度向右平移,⊙M以每秒2个单位长度的速度向右平移,
解:∵直线以每秒3个单位的速度向右平移,⊙M以每秒2个单位长度的速度向右平移,
∴相当于⊙M静止,直线以每秒1个单位的速度向右平移,
直线y=-$\frac{4}{3}$x-$\frac{4}{3}$与x轴的交点A的坐标为(-1,0),
由题意可知,⊙M的半径为3,设⊙M与x轴相切于点D.
在直角三角形AMD中,AD=4,DM=3,
由勾股定理得,AM=5,AE=5-3=2,
当直线l与⊙M相切于E时,直线交x轴于C,
△ADM∽△AEC,
AC:AM=AE:AD,
即AC:5=2:4,
解得AC=2.5,
∴当t=2.5s时,直线l与⊙M相切;
当直线l与⊙M相切于点F时,直线交x轴于G,
△ADM∽△AFG,
AG:AM=AF:AD,
即AG:5=8:4,
解得:AG=10,
∴当t=10时,直线l与⊙M相切,
故答案为:2.5或10.
点评 本题考查的是直线与圆的关系,通过分析得到直线的相对速度是解题的关键,解答时,注意运用分情况讨论的思想,正确运用相似三角形的性质也是重点.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
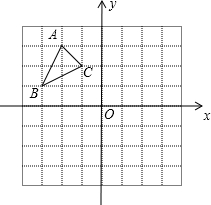
 如图,在平面直角坐标系中,O是原点,已知A(4,3),P是y轴上的动点,当点O,A,P三点组成的三角形为等腰三角形时,求出所有符合条件的点P坐标.
如图,在平面直角坐标系中,O是原点,已知A(4,3),P是y轴上的动点,当点O,A,P三点组成的三角形为等腰三角形时,求出所有符合条件的点P坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
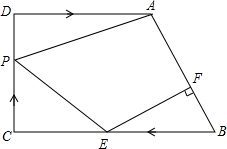 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com