
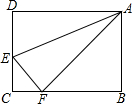
 如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.
如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2. 分析 首先根据折叠可以得到△ADE≌△AFE,所以求△AEF的面积是求△ADE的面积,而根据全等三角形的性质可以得到AD=AF,在直角三角形ABF中利用勾股定理可以求出BF,再利用已知条件可以求出FC,最后在直角三角形CEF 中利用勾股定理建立方程即可求出CE,然后求出DE即可求出△AEF的面积.
解答 解:∵将△ADE沿AE折叠后,点D正好落在BC边上的F处,
∴△ADE≌△AFE,
∴S△AEF=S△ADE,AD=AF,EF=DE,
在Rt△ABF中,
∵AB=8cm,AD=10cm=AF,
∴BF=6cm,
∴CF=BC-BF=AD-BF=4cm,
设DE=x,那么CE=8-x,EF=x,
∴在Rt△CEF中,
(8-x)2+42=x2,
∴x=5,
∴S△AEF=S△ADE=$\frac{1}{2}$AD×DE=25(cm2).
故答案为:25.
点评 本题考查图形的折叠与拼接,同时考查了矩形的基本知识,解题时应分别对每一个图形进行仔细分析,难度不大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
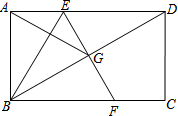 已知在矩形ABCD中,点E为边AD上一点,点A关于BE的对称点G位于对角线BD上,EG的延长线交边BC于点F.
已知在矩形ABCD中,点E为边AD上一点,点A关于BE的对称点G位于对角线BD上,EG的延长线交边BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
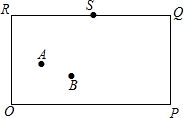 下面设想用电脑模拟台球游戏,为简单起见,约定:
下面设想用电脑模拟台球游戏,为简单起见,约定:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
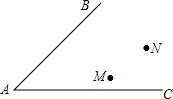 如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个饮水供应点P,使P到两条道路的距离相等,且使PM=PN.有一同学说:“只要作一个角平分线、一条线段的垂直平分线,这个茶水供应点的位置就确定了”,你认为这位同学说得对吗?请说明理由,并通过作图找出这一点,不写作法,保留作图痕迹.
如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个饮水供应点P,使P到两条道路的距离相等,且使PM=PN.有一同学说:“只要作一个角平分线、一条线段的垂直平分线,这个茶水供应点的位置就确定了”,你认为这位同学说得对吗?请说明理由,并通过作图找出这一点,不写作法,保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
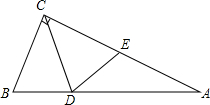 如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.
如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
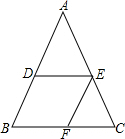 如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.
如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3•a2=a6 | B. | (-a3)2=a6 | C. | 2a+3a2=5a3 | D. | $3{a^3}÷2a=\frac{3}{2}{a^3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com