
| A. | 6 | B. | 12 | C. | 24 | D. | 27 |
分析 先将等式化成(x+1)(y+1)(z+1)=2013,然后分三种情况讨论得出非负整数解的可能,最后加起来即可.
解答 解:∵xyz+xy+xz+yz+x+y+z
=(xyz+yz)+(xy+y)+(xz+z)+(x+1)-1
=yz(x+1)+y(x+1)+z(x+1)+(x+1)-1
=(x+1)(yz+y+z+1)-1
=(x+1)[y(z+1)+(z+1)]-1
=(x+1)(y+1)(z+1)-1
=2012,
∴(x+1)(y+1)(z+1)=2013,
∵x,y,z都大于0,
①当x+1,y+1,z+1中没有一个等于1时,∴2013=3×11×61,共有6种;
②当x+1,y+1,z+1中有一个等于1时,
Ⅰ、当x+1=1时,即x=0时,∴2013=3×671=11×183=61×33,有6种,
Ⅱ、当y+1=1时,即y=0时,∴2013=3×671=11×183=61×33,有6种,
Ⅲ、当z+1=1时,即z=0时,∴2013=3×671=11×183=61×33,有6种,
③当x+1,y+1,z+1中有两个等于1时,共3种,
综上:4×6+3=27种,
故选D.
点评 此题是非一次不定方程,主要考查了分组,分类讨论,解本题的关键是得出(x+1)(y+1)(z+1)=2013,也是解本题的难道.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 镇江某中学教师每天乘坐公交车上班.如图是该教师坐在公交车上透过前面车辆的后窗玻璃拍摄到的该车的车号.若212路公交车途径镇江十中,215路途径姚桥中学,512路途径大港中学,515路途径京口中学,那么该教师的工作地点是( )
镇江某中学教师每天乘坐公交车上班.如图是该教师坐在公交车上透过前面车辆的后窗玻璃拍摄到的该车的车号.若212路公交车途径镇江十中,215路途径姚桥中学,512路途径大港中学,515路途径京口中学,那么该教师的工作地点是( )| A. | 镇江十中 | B. | 姚桥中学 | C. | 大港中学 | D. | 京口中学 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
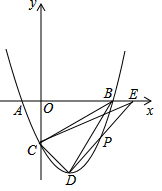 如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D位抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D位抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com