
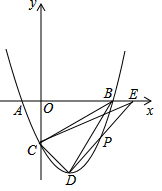
 如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D位抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D位抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).分析 (1)由抛物线已知,则可求三角形OBC的各个顶点,易知三角形形状及内角.
(2)因为抛物线已固定,则S四边形OCDB固定,对于坐标系中的不规则图形常用分割求和、填补求差等方法求面积,本图形过顶点作x轴的垂线及可将其分为直角梯形及直角三角形,面积易得.由此可得E点坐标,进而可求ED直线方程,与抛物线解析式联立求解即得P点坐标.
解答 解:(1)∵y=x2-2x-3=(x-3)(x+1),
∴由题意得,A(-1,0),B(3,0),C(0,-3),D(1,-4).
在Rt△OBC中,
∵OC=OB=3,
∴△OBC为等腰直角三角形,
∴∠OBC=45°.
(2)如图1,过点D作DH⊥x轴于H,
此时S四边形OCDB=S梯形OCDH+S△HBD,
∵OH=1,OC=3,HD=4,HB=2,
∴S梯形OCDH=$\frac{1}{2}$•(OC+HD)•OH=$\frac{7}{2}$,
S△HBD=$\frac{1}{2}$•HD•HB=4,
∴S四边形OCDB=$\frac{15}{2}$.
∴S△OCE=S四边形OCDB=$\frac{15}{2}$=$\frac{1}{2}$•OC•OE,
∴OE=5,
∴E(5,0).
设lDE:y=kx+b,
∵D(1,-4),E(5,0),
∴$\left\{\begin{array}{l}{k+b=-4}\\{5k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-5}\end{array}\right.$,
∴lDE:y=x-5.
∵DE交抛物线于P,设P(x,y),
∴x2-2x-3=x-5,
解得 x=2 或x=1(D点,舍去),
∴xP=2,代入lDE:y=x-5,
∴P(2,-3).
点评 本题考查了抛物线与x轴的交点,熟练掌握待定系数法求直线解析式、直角三角形性质及割补法求四边形的面积、直线和抛物线交点问题是解题的关键.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论的个数是( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一天硬化的多 | B. | 第二天硬化的多 | C. | 两天硬化一样多 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-6)2=34 | B. | (x+6)2=34 | C. | (x-3)2=7 | D. | (x-3)2=11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com