
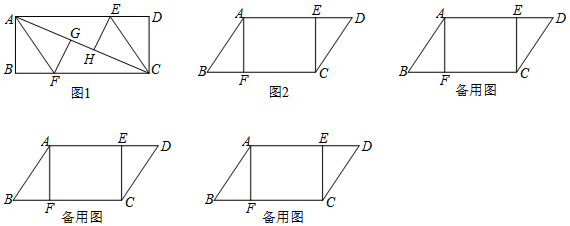
分析 (1)根据内错角相等得出AF∥CE,由两对应边互相平行得出AFCE是平行四边形,即可得出AE=CF;
(2)①当P点在BF上,Q点在ED上时,能构成平行四边形,根据平行四边形的性质,列出方程求解即可;
②分三种情况:当点P在AF上,Q点在CE上时,AP=CQ;当点P在BF上,Q点在DE上时,AQ=CP;当点P在AB上,Q点在CD上时,AP=CQ,分别得出a与b满足的数量关系式.
解答 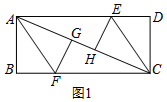 解:(1)如图1,∵四边形ABCD是矩形,
解:(1)如图1,∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BAC=∠DCA,
由折叠的性质可知,∠FAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$∠DCA=∠ECA,
∴AF∥CE,
∴四边形AFCE是平行四边形,
∴AE=CF.
故答案为:=;
(2)①∵在平行四边形ABCD中,△ABF≌△CDE,
∴AE=CF,BF=DE=6cm,AB=CD=10cm,
∵如图2,当P点在BF上,Q点在ED上,以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∴FP=EQ,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PF=5t-8,QE=16-4t,
∴5t-8=16-4t,
解得t=$\frac{8}{3}$,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=$\frac{8}{3}$秒;
②由题意得,以A,C,P,Q四点的四边形是平行四边形时,点P、Q在相互平行的对边上,
分三种情况:
Ⅰ.如图3,当点P在AF上,Q点在CE上时,AP=CQ,
即a=24-b,得:a+b=24;
Ⅱ.如图4,当点P在BF上,Q点在DE上时,AQ=CP,
又∵AE=CF,
∴EQ=FP,
即16-b=a-8,得a+b=24;
Ⅲ.如图5,当点P在AB上,Q点在CD上时,AP=CQ,
即24-a=b,得a+b=24.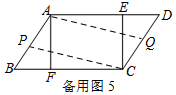
综上所述,a与b满足的数量关系式是a+b=24(ab≠0).
点评 本题属于四边形综合题,主要考查了平行四边形的判定与性质,全等三角形的性质,翻折变换的性质的综合应用,根据图形判断出以A、C、P、Q四点为顶点的四边形是平行四边形时,点P、Q的位置是解题的关键.解题时注意分类思想的运用.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
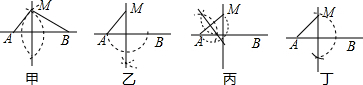
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论的个数是( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )
如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com