
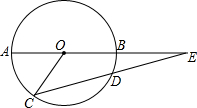
 已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数.
已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数. 分析 连接OD,根据等边对等角可得∠ODC=∠C=40°,再根据AB=2DE,OD=$\frac{1}{2}$AB可得OD=DE,再根据三角形外角的性质可得∠E的度数,进而可得∠AOC的度数.
解答  解:连接OD,
解:连接OD,
∵OC=OD,∠C=40°,
∴∠ODC=∠C=40°,
∵AB=2DE,OD=$\frac{1}{2}$AB,
∴OD=DE,
∵∠ODC是△DOE的外角,
∴∠E=∠EOD=$\frac{1}{2}$∠ODC=20°,
∵∠AOC是△COE的外角,
∴∠AOC=∠C+∠E=40°+20°=60°.
点评 此题主要考查了圆的认识,以及三角形内角与外角的关系,关键是掌握同圆中的半径是相等的.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 25(1+a%)2=18 | B. | 25(1-a%)2=18 | C. | 25(1-2a%)=18 | D. | 25(1-a2%)=18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
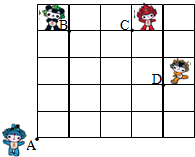 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com