
【题目】如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.

【答案】(1)证明见解析;(2)CG=2.
【解析】
本题需先连接EC、EB,根据AE是∠CAB的平分线,得出EG=EF,再根据ED垂直平分BC,得出Rt△CGE≌Rt△BFE,从而证出BF=CG;
本题根据AE是∠CAB的平分线,得出∠FAE=∠GAE,再根据EF⊥AB于点F,EG⊥AC于点G,得出∠AFE=∠AGE ,即可证得△AFE≌△AGE ,从而得到AF=AG,
设BF=CG=x, AG=AF=y,组成二元一次方程组即可求解.
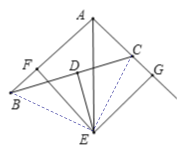
(1)连接EC、EB
![]() AE是∠CAB的平分线,
AE是∠CAB的平分线,
EF⊥AB于点F,EG⊥AC于点G,
![]() EG=EF
EG=EF
![]() 点D是BC的中点,ED垂直BC
点D是BC的中点,ED垂直BC
∴ED垂直平分BC,
![]() EC=EB
EC=EB
![]() Rt△CGE≌Rt△BFE(HL),
Rt△CGE≌Rt△BFE(HL),
![]() BF=CG
BF=CG
(2)![]() AE是∠CAB的平分线
AE是∠CAB的平分线
∴∠FAE=∠GAE
∵EF⊥AB于点F,EG⊥AC
∴∠AFE=∠AGE=90°
在△AFE和△AGE中
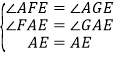 ,
,
∴△AFE≌△AGE(AAS)
∴AF=AG
设BF=CG=x, AG=AF=y
∴AB=AF+BF=x+y=10
AC=AG-CG=y-x=6
∴![]()
解得![]()
∴CG=BF=2.


科目:初中数学 来源: 题型:
【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为![]() 元时,每天能卖出
元时,每天能卖出![]() 串,在此基础上,每加价
串,在此基础上,每加价![]() 元李大妈每天就会少卖出
元李大妈每天就会少卖出![]() 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为![]() 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是![]() 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了第四章《基本的平面图形》的知识后,小明将自己手中的一副三角板的两个直角顶点叠放在一起拼成如下的图形1和图形2.
(1)在图1中,当AD平分∠BAC时,小明认为此时AB也应该平分∠FAD,请你通过计算判断小明的结论是否正确.
(2)小明还发现:只要AD在∠BAC的内部,当△ABC绕直角顶点A旋转时,总有∠FAB=∠DAC(见图2),请你判断小明的发现是否正确,并简述理由.
(3)在图2中,当∠FAC=x,∠BAD=y,请你探究x与y的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)若图中一个小正方形边长为一个单位长度,请写出各点的坐标:
A1 ;B1 ;C1 ;
(3)求△A1B1C1的面积.
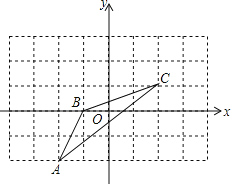
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,以
,以![]() 为直径在第一象限内作半圆,
为直径在第一象限内作半圆,![]() 为半圆上一点,连接
为半圆上一点,连接![]() 并延长至
并延长至![]() ,使
,使![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,已知
,已知![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点.
三点.

![]() ________°.
________°.
![]() 求抛物线的函数表达式.
求抛物线的函数表达式.
![]() 若
若![]() 为抛物线上位于第一象限内的一个动点,以
为抛物线上位于第一象限内的一个动点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形面积记作
为顶点的四边形面积记作![]() ,则
,则![]() 取何值时,相应的点
取何值时,相应的点![]() 有且只有
有且只有![]() 个?
个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师给学生出了一道题:求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=![]() ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”你认为他们谁说的有道理?为什么?
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”你认为他们谁说的有道理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题:(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;
(x﹣1)(x4+x3+x2+x+1)=x5﹣1
…
根据前面的规律,回答下列问题:
(1)(x﹣1)(xn+xn﹣1+xn﹣2+…+x3+x2+x+1)=_____.
(2)当x=3时,(3﹣1)(32015+32014+32013+…+33+32+3+1)=______.
(3)求:22014+22013+22012+…+23+22+2+1的值.(请写出解题过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com