
【题目】我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.
(1)试举一个例子来判断上述猜测结论是否成立
(2)若![]() 与
与![]() 互为相反数,求1﹣
互为相反数,求1﹣![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】平面上有n条直线,其中没有两条直线互相平行(即每两条直线都相交),也没有三条或三条以上的直线通过同一点.试求:
(1)这n条直线共有多少个交点?
(2)这n条直线把平面分割为多少块区域?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=![]() ,b=
,b=![]() ,c=
,c=![]() ; ②a=6,b=8,c=10; ③a=7,b=24,c=25;
; ②a=6,b=8,c=10; ③a=7,b=24,c=25;
④a=2,b=3,c=4.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨辉是我国南宋时期杰出的数学家和教育家,下图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: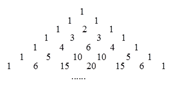
(1)图中给出了七行数字,根据构成规律,第8行中从左边数第3个数是;
(2)利用不完全归纳法探索出第n行中的所有数字之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
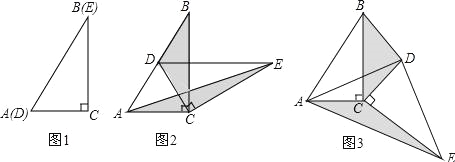
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=α,若固定△ABC,将△DEC绕点C旋转.
(1)当△DEC绕点C旋转到点D恰好落在AB边上时,如图2,则此时旋转角为 (用含的式子表示).
(2)当△DEC绕点C旋转到如图3所示的位置时,小杨同学猜想:△BDC的面积与△AEC的面积相等,试判断小杨同学的猜想是否正确,若正确,请你证明小杨同学的猜想.若不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据方程5x+2=6x-8编写了一道应用题.请你把空缺的部分补充完整.
某手工小组计划教师节前做一批手工品赠给老师,如果每人做5个,那么就比计划少2个; .请问手工小组有几人?(设手工小组有x人)
查看答案和解析>>
科目:初中数学 来源: 题型:
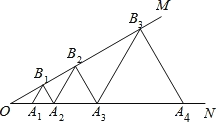
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
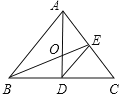
【题目】如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线的结论中正确的有_________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com