
【题目】如图,抛物线y=ax2+bx﹣3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=﹣1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).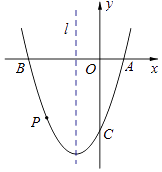
(1)直接写出抛物线的解析式;
(2)小唐探究点P的位置时发现:当动点N在对称轴l上时,存在PB⊥NB,且PB=NB的关系,请求出点P的坐标;
(3)是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值;若不存在,请说明理由.
【答案】
(1)
解:∵A(1,0),对称轴l为x=﹣1,
∴B(﹣3,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=x2+2x﹣3;
(2)
解:如图1,过点P作PM⊥x轴于点M,
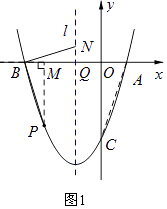
设抛物线对称轴l交x轴于点Q.
∵PB⊥NB,∴∠PBN=90°,
∴∠PBM+∠NBQ=90°.
∵∠PMB=90°,
∴∠PBM+∠BPM=90°.
∴∠BPM=∠NBQ.
又∵∠BMP=∠BNQ=90°,PB=NB,
∴△BPM≌△NBQ.
∴PM=BQ.
∵抛物线y=x2+2x﹣3与x轴交于点A(1,0)和点B,且对称轴为x=﹣1,
∴点B的坐标为(﹣3,0),点Q的坐标为(﹣1,0).∴BQ=2.∴PM=BQ=2.
∵点P是抛物线y=x2+2x﹣3上B、C之间的一个动点,
∴结合图象可知点P的纵坐标为﹣2,
将y=﹣2代入y=x2+2x﹣3,得﹣2=x2+2x﹣3,
解得x1=﹣1﹣ ![]() ,x2=﹣1+
,x2=﹣1+ ![]() (舍去),
(舍去),
∴此时点P的坐标为(﹣1﹣ ![]() ,﹣2)
,﹣2)
(3)
解:存在.
如图2,连接AC.
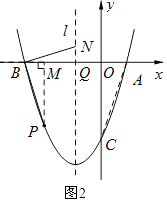
可设点P的坐标为(x,y)(﹣3<x<0),则y=x2+2x﹣3,
∵点A(1,0),∴OA=1.
∵点C是抛物线与y轴的交点,
∴令x=0,得y=﹣3.即点C(0,﹣3).
∴OC=3.
由(2)可知S四边形PBAC=S△BPM+S四边形PMOC+S△AOC
= ![]() BMPM+
BMPM+ ![]() (PM+OC)OM+
(PM+OC)OM+ ![]() OAOC
OAOC
= ![]() (x+3)(﹣y)+
(x+3)(﹣y)+ ![]() (﹣y+3)(﹣x)+
(﹣y+3)(﹣x)+ ![]() ×1×3
×1×3
=﹣ ![]() y﹣
y﹣ ![]() x+
x+ ![]() .
.
将y=x2+2x﹣3代入可得S四边形PBAC=﹣ ![]() (x2+2x﹣3)﹣
(x2+2x﹣3)﹣ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() .
.
∵﹣ ![]() <0,﹣3<x<0,
<0,﹣3<x<0,
∴当x=﹣ ![]() 时,S四边形PBAC有最大值
时,S四边形PBAC有最大值 ![]() .此时,y=x2+2x﹣3=﹣
.此时,y=x2+2x﹣3=﹣ ![]() .
.
∴当点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )时,四边形PBAC的面积最大,最大值为
)时,四边形PBAC的面积最大,最大值为 ![]() .
.
【解析】(1)由对称轴可求得B点坐标,结合A、B两点坐标,利用待定系数法可求得抛物线解析式;(2)过点P作PM⊥x轴于点M,设抛物线对称轴l交x轴于点Q.可证明△BPM≌△NBQ,则可求得PM=BQ,可求得P点的纵坐标,利用抛物线解析式可求得P点坐标;(3)连接AC,设出P点坐标,则可表示出四边形PBAC的面积,再利用二次函数的性质可求得其最大值.


科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,事实上,小明的表示方法是有道理的,因为
的小数部分,事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是
的整数部分是1,将这个数减去其整数部分,差就是![]() 的小数部分,又例如:∵22<(
的小数部分,又例如:∵22<(![]() )2<32,即2<
)2<32,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2).
﹣2).
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣![]() 的值.
的值.
(3)已知x是3+![]() 的整数部分,y是其小数部分,直接写出x﹣y的值.
的整数部分,y是其小数部分,直接写出x﹣y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE≌△CAD;
(2)若AD=25cm,BE=8cm,求DE的长.
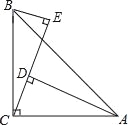
查看答案和解析>>
科目:初中数学 来源: 题型:
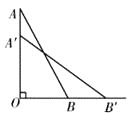
【题目】一个25米长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24米,如果梯子的顶端A沿墙下滑4米,那么梯子底端B也外移4米,对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
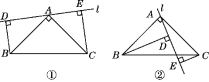
【题目】如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A旋转,BD⊥l于D,CE⊥l于E.
(1)试说明:DE=BD+CE.
(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
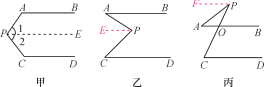
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).
x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A、B,且B点的坐标为(2,0).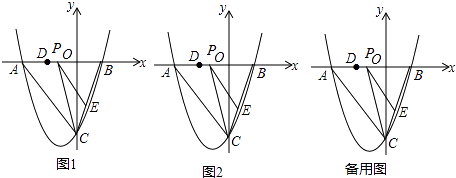
(1)求抛物线的解析式;
(2)若点P是AB上的一个动点,过点P作PE∥AC交BC于点E,连接CP,求△PCE面积最大时P点的坐标;
(3)在(2)的条件下,若点D为OA的中点,点M是线段AC上一点,当△OMD为等腰三角形时,连接MP、ME,把△MPE沿着PE翻折,点M的对应点为点N,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com