
【题目】如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A旋转,BD⊥l于D,CE⊥l于E.
(1)试说明:DE=BD+CE.
(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.
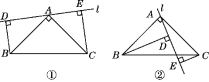
【答案】(1) 见解析; (2)(1)中结论不成立.DE=BD-CE. 探究过程见解析.
【解析】
(1)由AAS证明△ABD≌△CAE,得到BD=AE,AD=CE,即可解决问题.(2)由AAS证明证明△ABD≌△CAE,得出BD=AE,AD=CE,即可得出结论.
(1)因为BD⊥l,CE⊥l,
所以∠ADB=∠AEC=90°.
所以∠DBA+∠BAD=90°.
又因为∠BAC=90°,
所以∠BAD+∠CAE=90°.
所以∠DBA=∠CAE.
因为AB=AC,∠ADB=∠CEA=90°,
所以△ABD≌△CAE(AAS).
所以AD=CE,BD=AE.
则AD+AE=BD+CE,
即DE=BD+CE.
(2)(1)中结论不成立.
DE=BD-CE.
同(1)说明△ABD≌△CAE,
所以BD=AE,AD=CE.
又因为AE-AD=DE,
所以DE=BD-CE.


科目:初中数学 来源: 题型:
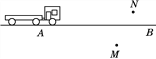
【题目】如图,M,N为坐落于公路两旁的村庄,如果一辆施工的机动车由A向B行驶,产生的噪音会对两个村庄造成影响.
(1)当施工车行驶到何处时,产生的噪音分别对两个村庄影响最大?在图中标出来.
(2)当施工车从A向B行驶时,产生的噪音对M,N两个村庄的影响情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习过反比例函数y= ![]() 的图象和性质,请回顾研究它的过程,对函数y=
的图象和性质,请回顾研究它的过程,对函数y= ![]() 进行探索.下列结论:
进行探索.下列结论:
①图象在第一、二象限,②图象在第一、三象限,
③图象关于y轴对称,④图象关于原点对称,
⑤当x>0时,y随x增大而增大;当x<0时,y随x增大而增大,
⑥当x>0时,y随x增大而减小;当x<0时,y随x增大而增大,
是函数y= ![]() 的性质及它的图象特征的是: . (填写所有正确答案的序号)
的性质及它的图象特征的是: . (填写所有正确答案的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
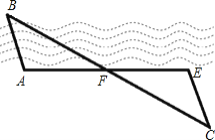
【题目】如图,小明和小月两家位于A,B两处隔河相望,要测得两家之间的距离,小明设计方案如下:
①从点A出发沿河岸画一条射线AM;
②在射线AM上截取AF=FE;
③过点E作EC∥AB,使B,F,C在一条直线上;
④CE的长就是A,B间的距离.
(1)请你说明小明设计的原理.
(2)如果不借助测量仪,小明的设计中哪一步难以实现?
(3)你能设计出更好的方案吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3与x轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为x=﹣1,点P是抛物线上B,C之间的一个动点(点P不与点B,C重合).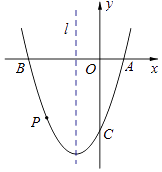
(1)直接写出抛物线的解析式;
(2)小唐探究点P的位置时发现:当动点N在对称轴l上时,存在PB⊥NB,且PB=NB的关系,请求出点P的坐标;
(3)是否存在点P使得四边形PBAC的面积最大?若存在,请求出四边形PBAC面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BE平分∠ABC,交AC边于点E,ED⊥AB,垂足为D.若△ABC的周长为12,△ADE的周长为6,则BC的长为( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示;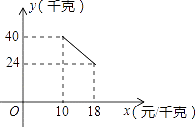
(1)求y(千克)与销售价x的函数关系式;
(2)该经销商想要获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为10,B是数轴上位于点A左侧一点,且AB=30,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
![]()
(1)数轴上点B表示的数是________,点P表示的数是________(用含![]() 的代数式表示);
的代数式表示);
(2)若M为线段AP的中点,N为线段BP的中点,在点P运动的过程中,线段MN的长度会发生变化吗?如果不变,请求出这个长度;如果会变化,请用含![]() 的代数式表示这个长度;
的代数式表示这个长度;
(3)动点Q从点B处出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时与点Q相距4个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com