考点:解分式方程
专题:
分析:(1)把分式方程去分母变成整式方程,求出整式方程的解,最后进行检验即可;
(2)把分式方程去分母变成整式方程,求出整式方程的解,最后进行检验即可;
(3)把分式方程去分母变成整式方程,求出整式方程的解,最后进行检验即可;
(4)把分式方程去分母变成整式方程,求出整式方程的解,最后进行检验即可.
解答:解:(1)方程两边都乘以x(x+1)得:6x=x+5,
解得:x=5,
检验:当x=5时,x(x+5)≠0,所以x=5是原方程的解,
即原方程的解为x=5;
(2)方程两边都乘以(x+1)(x-2)得:x-2-2(x+1)=0,
解得:x=-4,
检验:当x=-4时,(x+1)(x-2)≠0,所以x=-4是原方程的解,
即原方程的解为x=-4;
(3)方程两边都乘以x(x+1)(x-1)得:7(x-1)+3(x+1)=6x,
解得:x=1,
检验:当x=1时,x(x+1)(x-1)=0,所以x=1不是原方程的解,
即原方程无解;
(4)方程两边都乘以2x-5得:x-(2x-5)=-5,
解得:x=0,
检验:当x=0时,2x-5≠0,所以x=0是原方程的解,
即原方程的解为x=0.
点评:本题考查了解分式方程的应用,解此题的关键是能把分式方程转化成整式方程,题目比较好,难度适中.



 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案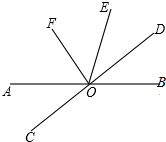 如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.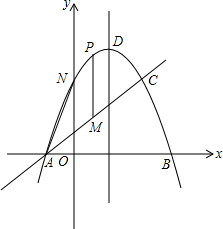 如图,已知抛物线y=-x2+2x+3与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N,抛物线的对称轴是直线x=1,其顶点为D(1,4)
如图,已知抛物线y=-x2+2x+3与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N,抛物线的对称轴是直线x=1,其顶点为D(1,4)