
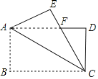
ЁОЬтФПЁПШчЭМЃЌдкЕШбќжБНЧЁїABCжаЃЌЁЯCЪЧжБНЧЃЌЕуAдкжБЯпMNЩЯЃЌЙ§ЕуCзїCEЁЭMNгкЕуEЃЌЙ§ЕуBзїBFЁЭMNгкЕуFЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБCЃЌBСНЕуОљдкжБЯпMNЕФЩЯЗНЪБЃЌ
ЂйжБНгаДГіЯпЖЮAEЃЌBFгыCEЕФЪ§СПЙиЯЕЃЎ
ЂкВТВтЯпЖЮAFЃЌBFгыCEЕФЪ§СПЙиЯЕЃЌВЛБиаДГіжЄУїЙ§ГЬЃЎ
ЃЈ2ЃЉНЋЕШбќжБНЧЁїABCШЦзХЕуAЫГЪБеыа§зЊжСЭМ2ЮЛжУЪБЃЌЯпЖЮAFЃЌBFгыCEгжгадѕбљЕФЪ§СПЙиЯЕЃЌЧыаДГіФуЕФВТЯыЃЌВЂаДГіжЄУїЙ§ГЬЃЎ
ЃЈ3ЃЉНЋЕШбќжБНЧЁїABCШЦзХЕуAМЬаја§зЊжСЭМ3ЮЛжУЪБЃЌBFгыACНЛгкЕуGЃЌШєAF=3ЃЌBF=7ЃЌжБНгаДГіFGЕФГЄЖШЃЎ
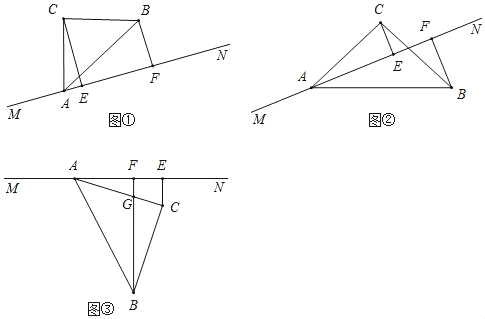
ЁОД№АИЁПЃЈ1ЃЉЂйAE+BF =ECЃЛЂкAF+BF=2CEЃЛЃЈ2ЃЉAFЉBF=2CEЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉFG=![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйжЛвЊжЄУїЁїACEЁеЁїBCDЃЈAASЃЉЃЌЭЦГіAE=BDЃЌCE=CDЃЌЭЦГіЫФБпаЮCEFDЮЊе§ЗНаЮЃЌМДПЩНтОіЮЪЬтЃЛ
ЂкРћгУЂйжаНсТлМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЪзЯШжЄУїBF-AF=2CEЃЎгЩAF=3ЃЌBF=7ЃЌЭЦГіCE=EF=2ЃЌAE=AF+EF=5ЃЌгЩFGЁЮECЃЌПЩжЊ![]() ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉжЄУїЃКЂйШчЭМ1ЃЌЙ§ЕуCзіCDЁЭBFЃЌНЛFBЕФбгГЄЯпгкЕуDЃЌ
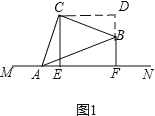
ЁпCEЁЭMNЃЌCDЁЭBFЃЌ
ЁрЁЯCEA=ЁЯD=90ЁуЃЌ
ЁпCEЁЭMNЃЌCDЁЭBFЃЌBFЁЭMNЃЌ
ЁрЫФБпаЮCEFDЮЊОиаЮЃЌ
ЁрЁЯECD=90ЁуЃЌ
гжЁпЁЯACB=90ЁуЃЌ
ЁрЁЯACB-ЁЯECB=ЁЯECD-ЁЯECBЃЌ
МДЁЯACE=ЁЯBCDЃЌ
гжЁпЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAC=BCЃЌ
дкЁїACEКЭЁїBCDжаЃЌ
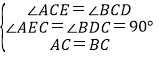 ЃЌ
ЃЌ
ЁрЁїACEЁеЁїBCDЃЈAASЃЉЃЌ
ЁрAE=BDЃЌCE=CDЃЌ
гжЁпЫФБпаЮCEFDЮЊОиаЮЃЌ
ЁрЫФБпаЮCEFDЮЊе§ЗНаЮЃЌ
ЁрCE=EF=DF=CDЃЌ
ЁрAE+BF=DB+BF=DF=ECЃЎ
ЂкгЩЂйПЩжЊЃКAF+BF=AE+EF+BF
=BD+EF+BF
=DF+EF
=2CEЃЌ
ЃЈ2ЃЉAF-BF=2CE
ЭМ2жаЃЌЙ§ЕуCзїCGЁЭBFЃЌНЛBFбгГЄЯпгкЕуGЃЌ
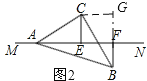
ЁпAC=BC
ПЩЕУЁЯAEC=ЁЯCGBЃЌ
ЁЯACE=ЁЯBCGЃЌ
дкЁїCBGКЭЁїCAEжаЃЌ
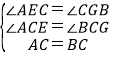 ЃЌ
ЃЌ
ЁрЁїCBGЁеЁїCAEЃЈAASЃЉЃЌ
ЁрAE=BGЃЌ
ЁпAF=AE+EFЃЌ
ЁрAF=BG+CE=BF+FG+CE=2CE+BFЃЌ
ЁрAF-BF=2CEЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуCзіCDЁЭBFЃЌНЛFBЕФгкЕуDЃЌ
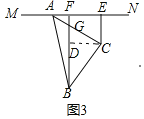
ЁпAC=BC
ПЩЕУЁЯAEC=ЁЯCDBЃЌ
ЁЯACE=ЁЯBCDЃЌ
дкЁїCBDКЭЁїCAEжаЃЌ
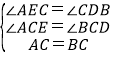 ЃЌ
ЃЌ
ЁрЁїCBDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрAE=BDЃЌ
ЁпAF=AE-EFЃЌ
ЁрAF=BD-CE=BF-FD-CE=BF-2CEЃЌ
ЁрBF-AF=2CEЃЎ
ЁпAF=3ЃЌBF=7ЃЌ
ЁрCE=EF=2ЃЌAE=AF+EF=5ЃЌ
ЁпFGЁЮECЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрFG=![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаГЄЭОПЭдЫеОУПЬь6ЃК30ЁЊ7ЃК30ПЊЭљФГЯиЕФШ§СОАрГЕЦБМлЯрЭЌЃЌЕЋГЕЕФЪцЪЪГЬЖШВЛЭЌ.аЁеХКЭаЁЭѕвђЪТашдкетвЛЪБЖЮГЫГЕШЅИУЯиЃЌЕЋВЛжЊЕРШ§СОГЕПЊРДЕФЫГађЃЌСНШЫВЩгУВЛЭЌЕФГЫГЕЗНАИЃКаЁеХЮоТлШчКЮОіЖЈГЫзјПЊРДЕФЕквЛСОГЕЃЌЖјаЁЭѕдђЪЧЯШЙлВьКѓЩЯГЕЃЌЕБЕквЛСОГЕПЊРДЪБЃЌЫћВЛЩЯГЕЃЌЖјЪЧзаЯИЙлВьГЕЕФЪцЪЪзДПі.ШєЕкЖўСОГЕЕФзДПіБШЕквЛСОГЕКУЃЌЫћОЭЩЯЕкЖўСОГЕЃЛШєЕкЖўСОГЕВЛШчЕквЛСОГЕЃЌЫћОЭЩЯЕкШ§СОГЕ.ШєАДетШ§СОГЕЕФЪцЪЪГЬЖШЗжЮЊгХЁЂжаЁЂВюШ§ЕШЃЌЧыФуЫМПМВЂЛиД№ЯТСаЮЪЬтЃК
(1)Ш§СОГЕАДГіЯжЕФЯШКѓЫГађЙВгаФФМИжжПЩФмЃП
(2)ЧыСаБэЗжЮіФФжжЗНАИГЫзјгХЕШГЕЕФПЩФмадДѓЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮфККЖўжаЙубХжабЇЮЊСЫСЫНтШЋаЃбЇЩњЕФПЮЭтдФЖСЕФЧщПіЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјаадФЖСЪБМфЕїВщЃЌЯжНЋбЇЩњУПбЇЦкЕФдФЖСЪБМфmЗжГЩAЁЂBЁЂCЁЂDЫФИіЕШМЖЃЈAЕШЃК90ЁмmЁм100ЃЌBЕШЃК80ЁмmЃМ90ЃЌCЕШЃК60ЁмmЃМ80ЃЌDЕШЃКmЃМ60ЃЛЕЅЮЛЃКаЁЪБЃЉЃЌВЂЛцжЦГіСЫШчЭМЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉCзщЕФШЫЪ§ЪЧЁЁ ЁЁШЫЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉБОДЮЕїВщЕФжкЪ§ЪЧЁЁ ЁЁЕШЃЌжаЮЛЪ§ТфдкЁЁ ЁЁЕШЃЎ
ЃЈ3ЃЉЙњМвЙцЖЈЃКЁАжааЁбЇУПбЇЦкЕФПЮЭтдФЖСЪБМфВЛЕЭгк60аЁЪБЁБЃЌШчЙћИУаЃНёФъга3500УћбЇЩњЃЌДяЕНЙњМвЙцЖЈЕФдФЖСЪБМфЕФШЫЪ§дМгаЁЁ ЁЁШЫЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈ2ЃЌЉ1ЃЉЃЌBЃЈ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈ2ЃЌЉ1ЃЉЃЌBЃЈ![]() ЃЌnЃЉСНЕуЃЌжБЯпy=2гыyжсНЛгкЕуCЃЎ
ЃЌnЃЉСНЕуЃЌжБЯпy=2гыyжсНЛгкЕуCЃЎ

ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
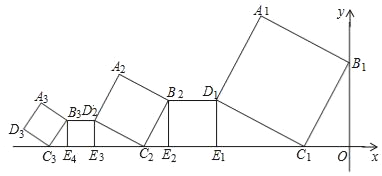
ЁОЬтФПЁПвЛзще§ЗНаЮАДШчЭМЫљЪОЕФЗНЪНЗХжУЃЌЦфжаЖЅЕуB1дкyжсЩЯЃЌЖЅЕуC1ЃЌE1ЃЌE2ЃЌC2ЃЌE3ЃЌE4ЃЌC3ЁЁдкxжсЩЯЃЌвбжЊе§ЗНаЮA1B1C1D1ЕФЖЅЕуC1ЕФзјБъЪЧЃЈЉ![]() ЃЌ0ЃЉЃЌЁЯB1C1O=60ЁуЃЌB1C1ЁЮB2C2ЁЮB3C3ЁЁдђе§ЗНаЮA2018B2018C2018D2018ЕФЖЅЕуD2018знзјБъЪЧ_____ЃЎ
ЃЌ0ЃЉЃЌЁЯB1C1O=60ЁуЃЌB1C1ЁЮB2C2ЁЮB3C3ЁЁдђе§ЗНаЮA2018B2018C2018D2018ЕФЖЅЕуD2018знзјБъЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁУїЮЊСЫВтСПДѓТЅABЕФИпЖШЃЌЫћДгЕуCГіЗЂЃЌбизХаБЦТУцCDзп260УзЕНЕуDДІЃЌВтЕУДѓТЅЖЅВПЕуAЕФбіНЧЮЊ37ЁуЃЌДѓТЅЕзВПЕуBЕФИЉНЧЮЊ45ЁуЃЌвбжЊаБЦТCDЕФЦТЖШЮЊi=1ЃК2.4ЃЎдђДѓТЅABЕФИпЖШдМЮЊЃЈЁЁЁЁЃЉУзЃЎ
ЃЈВЮПМЪщОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЉ

A. 170 B. 175 C. 180 D. 190
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃК
ЃЈ1ЃЉЛГіЁїABCЙигкyжсЕФЖдГЦЭМаЮЁїA1B1C1ЃЛ
ЃЈ2ЃЉЧыМЦЫуЁїABCЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГіЁїABCЙигкxжсЖдГЦЕФШ§НЧаЮЁїA2B2C2ЕФИїЕузјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮжНЦЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌ
ДІЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЕШгкЃЈ ЃЉ
ЕФГЄЕШгкЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫСЫНтАрМЖбЇЩњЪ§бЇПЮЧАдЄЯАЕФОпЬхЧщПіЃЌжЃРЯЪІЖдБОАрВПЗжбЇЩњНјааСЫЮЊЦквЛИідТЕФИњзйЕїВщЃЌЫћНЋЕїВщНсЙћЗжЮЊЫФРрЃКAЃККмКУЃЛBЃКНЯКУЃЛCЃКвЛАуЃЛDЃКВЛДяБъЃЌВЂНЋЕїВщНсЙћЛцжЦГЩвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉCРрХЎЩњгаЁЁ ЁЁУћЃЌDРрФаЩњгаЁЁ ЁЁУћЃЌНЋЩЯУцЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЁАПЮЧАдЄЯАВЛДяБъЁБЖдгІЕФдВаФНЧЖШЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ3ЃЉЮЊСЫЙВЭЌНјВНЃЌжЃРЯЪІЯыДгБЛЕїВщЕФAРрКЭDРрбЇЩњжаИїЫцЛњЛњГщШЁвЛЮЛЭЌбЇНјааЁАвЛАявЛЁБЛЅжњбЇЯАЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓГіЫљбЁСНЮЛЭЌбЇЧЁКУЪЧвЛФавЛХЎЭЌбЇЕФИХТЪЃЌ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com