
分析 (1)(2)(5)(6)(7)(8)根据有理数的混合运算的运算方法,求出每个算式的值各是多少即可.
(3)应用乘法交换律和加法结合律,求出算式的值是多少即可.
(4)应用乘法分配律,求出每个算式的值是多少即可.
解答 解:(1)24+(-14)+(-16)+8
=10+(-16)+8
=(-6)+8
=2
(2)(+$\frac{3}{4}}$)-(-$\frac{5}{4}}$)-|-3|
=2-3
=-1
(3)-54×2$\frac{1}{4}$÷(-4$\frac{1}{2}$)×$\frac{2}{9}$
=(-54×$\frac{2}{9}$)×2$\frac{1}{4}$÷(-4$\frac{1}{2}$)
=(-12)×(-$\frac{1}{2}$)
=6
(4)($\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$)×(-36)
=$\frac{1}{2}$×(-36)-$\frac{5}{9}$×(-36)+$\frac{7}{12}$×(-36)
=-18+20-21
=2-21
=-19
(5)-22×7-(-3)×6+5
=-28+18+5
=-10+5
=-5
(6)-18÷(-3)2+5×(-$\frac{1}{2}}$)3
=-18÷9+5×(-$\frac{1}{8}$)
=-2-$\frac{5}{8}$
=-2$\frac{5}{8}$
(7)|-2$\frac{1}{4}$|-(-$\frac{3}{4}$)+1-|1-$\frac{1}{2}$|
=(2$\frac{1}{4}$+$\frac{3}{4}$)+1-$\frac{1}{2}$
=3+1-$\frac{1}{2}$
=4-$\frac{1}{2}$
=3$\frac{1}{2}$
(8)-24+3×(-1)2000-(-2)2
=-16+3×1-4
=-13-4
=-17
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


科目:初中数学 来源: 题型:填空题
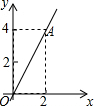 如图,将直线AO向上平移1个单位,得到一个一次函数的图象l1.
如图,将直线AO向上平移1个单位,得到一个一次函数的图象l1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平移和旋转都不改变图形的形状和大小 | |
| B. | 任意多边形都可以进行镶嵌 | |
| C. | 有两个角相等的四边形是平行四边形 | |
| D. | 对角线互相垂直的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-$\frac{1}{2}{x^2}$-x+3.
已知二次函数y=-$\frac{1}{2}{x^2}$-x+3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com