
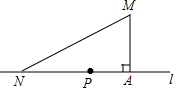
 如图,我校(点M)距公路(直线l)的距离(MA)为1km,在公路上距我校2km处有一车站(点N),我校拟在公路上建一个公交车停靠站(点P),以便于我校职工乘车上下班,要求停靠站到我校与车站的距离相等,请问:停靠站应建在什么位置?并计算停靠站到车站的距离.
如图,我校(点M)距公路(直线l)的距离(MA)为1km,在公路上距我校2km处有一车站(点N),我校拟在公路上建一个公交车停靠站(点P),以便于我校职工乘车上下班,要求停靠站到我校与车站的距离相等,请问:停靠站应建在什么位置?并计算停靠站到车站的距离. 分析 首先在Rt△AMN中,求出AN,设PN=PM=x,在Rt△PAM中,利用勾股定理列出方程即可解决问题.
解答 解:如图,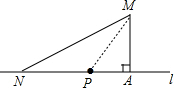
连接MP,在Rt△MAN中,MA=1,MN=2,由勾股定理得AN=$\sqrt{M{N}^{2}-A{M}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
设NP=xkm,则PM=xkm,
∴PA=($\sqrt{3}$-x)km,
在Rt△MAP中,由勾股定理得12+($\sqrt{3}$-x)2=x2,
解得x=$\frac{2\sqrt{3}}{3}$.
答:停靠站应建在线段AN上离点N的距离为$\frac{2\sqrt{3}}{3}$km处.
点评 本题考查勾股定理的应用,解题的关键是学会利用勾股定理构建方程解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)
如图,已知在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,-4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com