
ЁОЬтФПЁПШчЭМЃЌЕШбќШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
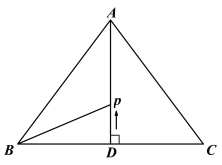
ЃЌ![]() ЃЌADЮЊЕзБпBCЩЯЕФИпЃЌЖЏЕу
ЃЌADЮЊЕзБпBCЩЯЕФИпЃЌЖЏЕу![]() ДгЕуDГіЗЂЃЌбиDAЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ
ДгЕуDГіЗЂЃЌбиDAЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ![]() ЃЌдЫЖЏЕН
ЃЌдЫЖЏЕН![]() ЕуЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ
ЕуЭЃжЙЃЌЩшдЫЖЏЪБМфЮЊ![]() ЃЌСЌНгBPЃЎ(0ЁмtЁм8)
ЃЌСЌНгBPЃЎ(0ЁмtЁм8)
ЃЈ1ЃЉЧѓADЕФГЄЃЛ
ЃЈ2ЃЉЩшЁїAPBЕФУцЛ§ЮЊyЃЈcmЃЉЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕУSЁїAPB:SЁїABC=1:3ЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЈ4ЃЉЪЧЗёДцдкФГвЛЪБПЬ![]() ЃЌЪЙЕУЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌШєДцдкЃЌЧѓГі
ЃЌЪЙЕУЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ8ЃЛЃЈ2ЃЉyЃН24Љ3tЃЈ0ЁмtЁм8ЃЉЃЛЃЈ3ЃЉДцдкЃЌ![]() ЃЛЃЈ4ЃЉДцдкЃЌ
ЃЛЃЈ4ЃЉДцдкЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЕШбќШ§НЧаЮЕФаджЪвдМАЙДЙЩЖЈРэНтОіЮЪЬтМДПЩЃЎ
ЃЈ2ЃЉИљОнyЃНSЁїAPBЃНSЁїABDЉSЁїPBDЃЌЛЏМђМЦЫуМДПЩЃЎ
ЃЈ3ЃЉгЩЬтвтSЁїAPBЃКSЁїABCЃН1ЃК3ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
ЃЈ4ЃЉгЩЬтвтЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌЭЦГіPAЃНPBЃЌдкRtЁїPBDжаЃЌИљОнPB2ЃНPD2+BD2ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉЁпABЃНACЃЌADЁЭBCЃЌ
ЁрBCЃНDCЃН6cmЃЌ
дкRtЁїABDжаЃЌЁпЁЯADBЃН90ЁуЃЌABЃН10cmЃЌBDЃН6cmЃЌ
ЁрADЃН![]() ЃН
ЃН![]() ЃН8ЃЈcmЃЉЃЎ
ЃН8ЃЈcmЃЉЃЎ
ЃЈ2ЃЉyЃНSЁїAPBЃНSЁїABDЉSЁїPBDЃН![]() ЁС6ЁС8Љ
ЁС6ЁС8Љ![]() ЁС6ЁСtЃНЉ3t+24ЃЎ
ЁС6ЁСtЃНЉ3t+24ЃЎ
ЁрyЃН24Љ3tЃЈ0ЁмtЁм8ЃЉЃЎ
ЃЈ3ЃЉЁпSЁїAPBЃКSЁїABCЃН1ЃК3ЃЌ
ЁрЃЈ24Љ3tЃЉЃК![]() ЁС12ЁС8ЃН1ЃК3ЃЌ
ЁС12ЁС8ЃН1ЃК3ЃЌ
НтЕУtЃН![]() ЃЎ
ЃЎ
ЁрТњзуЬѕМўЕФtЕФжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉгЩЬтвтЕуPдкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯЃЌ
ЁрPAЃНPBЃЌ
дкRtЁїPBDжаЃЌЁпPB2ЃНPD2+BD2ЃЌ
Ёрt2ЃНЃЈ8ЉtЃЉ2+62ЃЌ
НтЕУtЃН![]() ЃЎ
ЃЎ
ЁрТњзуЬѕМўЕФtЕФжЕЮЊ![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк2016ФъЁАЫЋЪЎвЛЁБЦкМфЃЌФГПьЕнЙЋЫОМЦЛЎзтгУМзЁЂввСНжжГЕСОПьЕнЛѕЮяЃЌДгЛѕЮяСПРДМЦЫуЃКШєзтгУСНжжГЕСОКЯдЫЃЌ10ЬьПЩвдЭъГЩШЮЮёЃЛШєЕЅЖРзтгУввжжГЕСОЃЌЭъГЩШЮЮёЕФЬьЪ§ЪЧЕЅЖРзтгУМзжжГЕСОЭъГЩШЮЮёЬьЪ§ЕФ2БЖЃЎ
(1)ЧѓМзЁЂввСНжжГЕСОЕЅЖРЭъГЩШЮЮёЗжБ№ашвЊЖрЩйЬьЃП
(2)вбжЊзтгУМзЁЂввСНжжГЕСОКЯдЫашзтН№65000дЊЃЌМзжжГЕСОУПЬьЕФзтН№БШввжжГЕСОУПЬьЕФзтН№Жр1500дЊЃЌЪдЮЪЃКзтМзКЭввСНжжГЕСОЁЂЕЅЖРзтМзжжГЕСОЁЂЕЅЖРзтввжжГЕСОетШ§жжзтГЕЗНАИжаЃЌФФвЛжжзтН№зюЩйЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуAЃЌCЃЌЮЊАыОЖЪЧ6ЕФЁбOЩЯСНЕуЃЌЕуBЮЊ![]() ЕФжаЕуЃЌвдЯпЖЮBAЃЌBCЮЊСкБпзїСтаЮABCDЃЌЪЙЕуDТфдкЁбOФкЃЈВЛКЌдВжмЩЯЃЉЃЌдђЯТСаНсТлЃКЂйжБЯпBDБиЙ§дВаФOЃЛЂкСтаЮABCDЕФБпГЄaЕФШЁжЕЗЖЮЇЪЧ0ЃМaЃМ10ЃЛЂлШєЕуDгыдВаФOжиКЯЃЌдђЁЯABC=120ЁуЃЛЂмШєDO=2ЃЌдђСтаЮABCDЕФБпГЄЮЊ
ЕФжаЕуЃЌвдЯпЖЮBAЃЌBCЮЊСкБпзїСтаЮABCDЃЌЪЙЕуDТфдкЁбOФкЃЈВЛКЌдВжмЩЯЃЉЃЌдђЯТСаНсТлЃКЂйжБЯпBDБиЙ§дВаФOЃЛЂкСтаЮABCDЕФБпГЄaЕФШЁжЕЗЖЮЇЪЧ0ЃМaЃМ10ЃЛЂлШєЕуDгыдВаФOжиКЯЃЌдђЁЯABC=120ЁуЃЛЂмШєDO=2ЃЌдђСтаЮABCDЕФБпГЄЮЊ![]() Лђ
Лђ![]() ЃЎЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЎЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. ЂйЂл B. ЂкЂлЂм C. ЂйЂлЂм D. ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇЮЊЗсИЛзлКЯЪЕМљЛюЖЏЃЌПЊЩшСЫЫФИіЪЕбщЪвШчЯТЃКAЃЎЮяРэЃЛBЃЎЛЏбЇЃЛCЃЎаХЯЂЃЛDЃЎЩњЮяЃЎЮЊСЫНтбЇЩњзюЯВЛЖФФИіЪЕбщЪвЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌУПЮЛБЛЕїВщЕФбЇЩњЖМбЁдёСЫвЛИіздМКзюЯВЛЖЕФЪЕбщЪвЃЌЕїВщКѓНЋЕїВщНсЙћЛцжЦГЩСЫШчЭМЭГМЦЭМЃЌЧыИљОнЭГМЦЭМЛиД№ЯТСаЮЪЬт
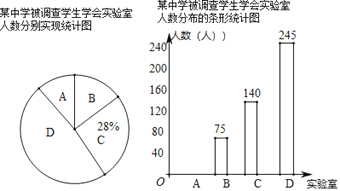
ЃЈ1ЃЉЧѓетДЮБЛЕїВщЕФбЇЩњШЫЪ§ЃЎ
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ3ЃЉЧѓГіЩШаЮЭГМЦЭМжаBЖдгІЕФдВаФНЧЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзввСНЕиЯрОр400ЧЇУзЃЌвЛСОЛѕГЕКЭвЛСОНЮГЕЯШКѓДгМзЕиГіЗЂЪЛЯђввЕиЃЌШчЭМЃЌЯпЖЮOAБэЪОЛѕГЕРыМзЕиЕФТЗГЬyЃЈЧЇУзЃЉгыЫљгУЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЌелЯпBCDБэЪОНЮГЕРыМзЕиЕФТЗГЬyЃЈЧЇУзЃЉгыxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЌИљОнЭМЯѓНтД№ЯТСаЮЪЬтЃК
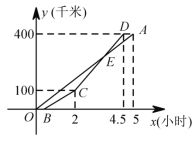
ЃЈ1ЃЉЧѓЯпЖЮCDЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉдкНЮГЕзЗЩЯЛѕГЕКѓЕНЕНДяввЕиЧАЃЌКЮЪБНЮГЕдкЛѕГЕЧА30ЧЇУзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧжЊЕРЃЌШЮвтвЛИігаРэЪ§гыЮоРэЪ§ЕФКЭЮЊЮоРэЪ§ЃЌШЮвтвЛИіВЛЮЊСуЕФгаРэЪ§гывЛИіЮоРэЪ§ЕФЛ§ЮЊЮоРэЪ§ЃЌЖјСугыЮоРэЪ§ЕФЛ§ЮЊСу.гЩДЫПЩЕУЃКШчЙћmx+n=0ЃЌЦфжаmЁЂnЮЊгаРэЪ§ЃЌxЮЊЮоРэЪ§ЃЌФЧУДm=0Чвn=0.
ЃЈ1ЃЉШчЙћ![]() ЃЌЦфжаaЁЂbЮЊгаРэЪ§ЃЌФЧУДa= ЃЌb= .
ЃЌЦфжаaЁЂbЮЊгаРэЪ§ЃЌФЧУДa= ЃЌb= .
ЃЈ2ЃЉШчЙћ![]() ЃЌЦфжаaЁЂbЮЊгаРэЪ§ЃЌЧѓa+2bЕФжЕ.
ЃЌЦфжаaЁЂbЮЊгаРэЪ§ЃЌЧѓa+2bЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌЕуMдкBAЕФбгГЄЯпЩЯЃЌMDЧаЁбOгкЕуDЃЌЙ§ЕуBзїBNЁЭMDгкЕуCЃЌСЌНгADВЂбгГЄЃЌНЛBNгкЕуNЃЎ
(1)ЧѓжЄЃКAB=BNЃЛ
(2)ШєЁбOАыОЖЕФГЄЮЊ3ЃЌcosB=![]() ЃЌЧѓMAЕФГЄЃЎ
ЃЌЧѓMAЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
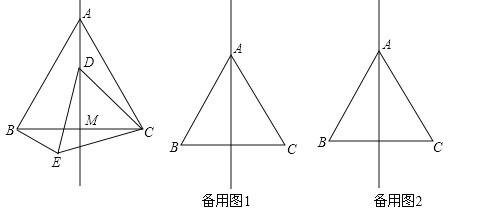
ЁОЬтФПЁПШчЭМЃЌдкЕШБпЁїABCжаЃЌЯпЖЮAMЮЊBCБпЩЯЕФжаЯпЃЎЖЏЕуDдкжБЯпAMЩЯЪБЃЌвдCDЮЊвЛБпдкCDЕФЯТЗНзїЕШБпЁїCDEЃЌСЌНсBEЃЎ
ЃЈ1ЃЉЧѓЁЯCAMЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЕуDдкЯпЖЮAMЩЯЪБЃЌЧѓжЄЃКЁїADCЁеЁїBECЃЛ
ЃЈ3ЃЉЕБЖЏDдкжБЯпAMЩЯЪБЃЌЩшжБЯпBEгыжБЯпAMЕФНЛЕуЮЊOЃЌЪдХаЖЯЁЯAOBЪЧЗёЮЊЖЈжЕЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬт6ЗжЃЉМзЁЂввСНШЫНјааУўХЦгЮЯЗЃЎЯжгаШ§еХаЮзДДѓаЁЭъШЋЯрЭЌЕФХЦЃЌе§УцЗжБ№БъгаЪ§зж2ЃЌ3ЃЌ5ЃЎНЋШ§еХХЦБГУцГЏЩЯЃЌЯДдШКѓЗХдкзРзгЩЯЃЎ
ЃЈ1ЃЉМзДгжаЫцЛњГщШЁвЛеХХЦЃЌМЧТМЪ§зжКѓЗХЛиЯДдШЃЌввдйЫцЛњГщШЁвЛеХЃЎЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓСНШЫГщШЁЯрЭЌЪ§зжЕФИХТЪЃЛ
ЃЈ2ЃЉШєСНШЫГщШЁЕФЪ§зжКЭЮЊ2ЕФБЖЪ§ЃЌдђМзЛёЪЄЃЛШєГщШЁЕФЪ§зжКЭЮЊ5ЕФБЖЪ§ЃЌдђввЛёЪЄЃЎетИігЮЯЗЙЋЦНТ№ЃПЧыгУИХТЪЕФжЊЪЖМгвдНтЪЭЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com