
【题目】如图,矩形 ABCD 中,点 G 是 AD 的中点,GE⊥CG 交 AB 于 E,BE=BC,连接 CE 交 BG 于 F,则∠BFC 等于_______.
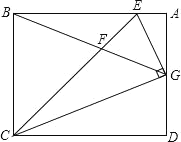
【答案】67.5
【解析】
判断出△BCE是等腰直角三角形,根据等腰直角三角形的性质可得∠BCE=∠BEC=45°,根据同角的余角相等求出∠AGE=∠DCG,然后根据两组角对应相等的两三角形相似求出△AGE和△DCG相似,根据相似三角形对应边成比例可得![]() ,再判断出△CDG和△CGE相似,根据相似三角形对应角相等可得∠DCG=∠GCE,然后求出∠DCG=22.5°,再根据矩形的对称性可得∠ABG=∠DCG,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
,再判断出△CDG和△CGE相似,根据相似三角形对应角相等可得∠DCG=∠GCE,然后求出∠DCG=22.5°,再根据矩形的对称性可得∠ABG=∠DCG,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
∵∵四边形ABCD是矩形,
∴∠A=∠D=∠ABC=90,
∵BE=BC,
∴△BCE是等腰直角三角形,
∴∠BCE=∠BEC=45,
∵GE⊥CG,
∴∠AGE+∠CGD=90,
∵∠DCG+∠CGD=90,
∴∠AGE=∠DCG,
又∵∠A=∠D=90,
∴△AGE∽△DCG,
∴![]() ,
,
∵G是AD的中点,
∴AG=DG,
∴![]() ,
,
∵∠D=∠CGE=90,
∴△CDG∽△CGE,
∴∠DCG=∠GCE=![]() (9045)=22.5,
(9045)=22.5,
∵G是AD的中点,
∴由矩形的对称性可知∠ABG=∠DCG=22.5,
由三角形的外角性质得,∠BFC=∠ABG+∠BEC=22.5+45=67.5.
故答案为:67.5.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
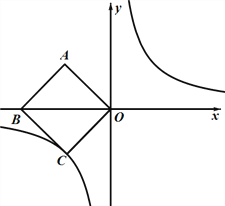
【题目】如图,在平面直角坐标系![]() 中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为
中,正方形ABCO的对角线BO在x 轴上,若正方形ABCO的边长为![]() ,点B在x负半轴上,反比例函数
,点B在x负半轴上,反比例函数![]() 的图象经过C点.
的图象经过C点.
(1)求该反比例函数的解析式;
(2)当函数值![]() >-2时,请直接写出自变量x的取值范围;
>-2时,请直接写出自变量x的取值范围;
(3)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为22m,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为( )
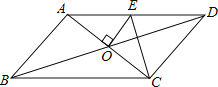
A. 8cmB. 9cmC. 10cmD. 11cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向东走100米到聪聪家,再向西走150米到青青家,再向东走200米到刚刚家,请问:
【1】聪聪家与刚刚家相距多远?
【2】如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出他们家与学校的大概位置(数轴上50米表示单位1).
【3】聪聪家向西210米所表示的数是多少?
【4】你认为可用什么办法求数轴上两点之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 的边长为 5,点 M 是边 BC 上的点,DE⊥AM 于点 E,BF∥DE,交 AM 于点 F.若E 是 AF 的中点,则 DE 的长为( )
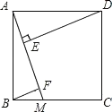
A.![]() B.2
B.2![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果![]() ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )
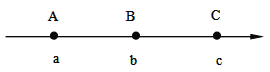
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上.向内放入两个半径为5 cm的钢球,测得上面一个钢球的最高点到底面的距离DC=16 cm(钢管的轴截面如图所示),则钢管的内径AD的长为_______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司4月份销售某厂家的汽车,在一定范围内每部汽车的进价与销售量有如下关系;若当月仅售出1辆汽车,则该部汽车的进价为25万元,每多售出1辆,所有售出的汽车的进价均降低0.2万元/辆,月底厂家根据销售量一次性返利给销售公司,销售量在10辆以内(含10辆),每辆返利0.6万元;销售量在10辆以上,每辆返利1.2万元.
(1)若该公司当月售出3辆汽车,则每辆汽车的进价为________万元;
(2)若该公司当月售出5辆汽车,且每辆汽车售价为![]() 元,则该销售公司该月盈利________万元(用含
元,则该销售公司该月盈利________万元(用含![]() 的代数式表示).
的代数式表示).
(3)如果汽车的售价为25.6万元/辆,该公司计划当月盈利16.8万元,那么需要售出多少辆汽车?(盈利销售利润+返利)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com