
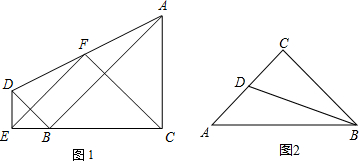
分析 (1)延长EF交CA的延长线于点G,由点F是AD的中点,得到AF=DF由已知条件△ACB与△BED都是等腰直角三角形,推出三角形全等的条件,关键直角三角形的性质得出结论.
(2)在AB上取E使BE=BC,由BD是等腰三角形ABC底角平分线,得到∠CBD=∠EBD,由BD=BD,推出三角形的全等△BCD≌△BED,得到CD=DE,由于AB=BC+CD,且AE=ED=DC,∠C=∠BED=2∠A=∠A+∠B=180°-∠C,得到结果∠C=90°.
解答  解:(1)如图1,延长EF交CA的延长线于点G,
解:(1)如图1,延长EF交CA的延长线于点G,
∵点F是AD的中点,
∴AF=DF
∵△ACB与△BED都是等腰直角三角形,
∴AC∥DE,
∴∠G=∠DEF,∠GAF=∠EDF,
在△AGF与△DEF中,$\left\{\begin{array}{l}{∠G=∠DEF}\\{∠GAF=∠EDF}\\{AF=DF}\end{array}\right.$,
∴△AGF≌△DEF,
∴DE=AG,点F是EG的中点,
∴EB=DE,CE=CG,
∵△GCE中,∠GCE=90°,
∴EF=CF,EF⊥CF;
(2)如图2,在AB上取E使BE=BC,
∵BD是等腰三角形ABC底角平分线,
∴∠CBD=∠EBD,
∵BD=BD,
在△BCD与△BED中,$\left\{\begin{array}{l}{BE=BC}\\{∠EBD=∠CBD}\\{BD=BD}\end{array}\right.$
∴△BCD≌△BED,
∴CD=DE,
∵AB=BC+CD,
且AE=ED=DC,∠C=∠BED=2∠A=∠A+∠B=180°-∠C,
∴∠C=90°.
点评 本题考查了等腰直角三角形的判定和性质,全等三角形的判定与性质,正确的作出辅助线构造全等三角形是解题的关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
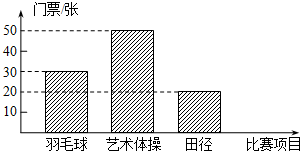 2010年5月20日上午10时起,2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分门票价格,如图为某公司购买的门票种类、数量所绘制成的条形统计图.
2010年5月20日上午10时起,2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分门票价格,如图为某公司购买的门票种类、数量所绘制成的条形统计图.| 比赛项目 | 票价(元/张) |
| 羽毛球 | 400 |
| 艺术体操 | 240 |
| 田径 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | 16 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )
如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com