
【题目】若x≠y,则下列各式不能成立的是( )
A.(x﹣y)2=(y﹣x)2
B.(x﹣y)3=﹣(y﹣x)3
C.(x+y)(y﹣x)=(x+y)(x﹣y)
D.(x+y)2=(﹣x﹣y)2
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】我们进入中学以来,已经学习过不少有关数据的统计量,例如_____________________等,它们分别从不同的侧面描述了一组数据的特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住世博会商机,某商店决定购进A、B两种世博会纪念品,若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出4000元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B钟纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 2016湖北鄂州第23题)某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
⑴(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
⑵(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
⑶(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,射线AB∥CD,∠CAB的角平分线交射线CD于点P1 . 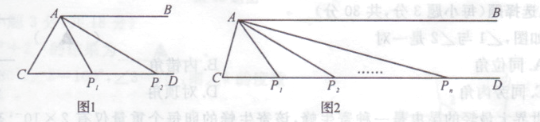
(1)若∠C=50°,求∠AP1C的度数.
(2)如图1,作∠P1AB的角平分线交射线CD于点P2 . 猜想∠AP1C与∠AP2C的数量关系,并说明理由.
(3)如图2,在(2)的条件下,依次作出∠P2AB的角平分线AP3 . ∠P3AB的角平分线AP4 , ……“∠Pn-1AB的角平分线APn . 其中点P3,P4…,Pn-1Pn都在射线CD上,若∠APnC=x,直接写出∠C的度数(用含x的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
查看答案和解析>>
科目:初中数学 来源: 题型:
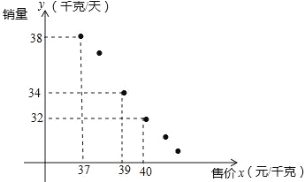
【题目】某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
(1)试求出y与x之间的一个函数关系式;
(2)利用(1)的结论:
①求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月(30天),若售价不低于30元/千克,则一次进货最多只能多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com