
【题目】如图![]() ,已知
,已知![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是
是![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .作
.作![]() 的外接圆
的外接圆![]() .设
.设![]() =
=![]() ,
,![]() =
=![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若![]() 是
是![]() 的切线,求
的切线,求![]() 的值;
的值;
(3)过点________作________![]() ________,垂足为________,交
________,垂足为________,交![]() ________于点________,直线________交________于点________(如图
________于点________,直线________交________于点________(如图![]() ).若________=
).若________=![]() ,则
,则![]() ________的值是________.
________的值是________.
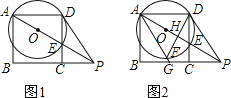
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明![]() ,利用相似比得到
,利用相似比得到![]() ,然后变形有
,然后变形有![]() ;
;
(2)连接![]() ,如图
,如图![]() ,根据圆周角定理得
,根据圆周角定理得![]() 是
是![]() 的直径,再利用切线的性质得
的直径,再利用切线的性质得![]() ,接着证明
,接着证明![]() ,利用相似比得到
,利用相似比得到![]() ,即
,即![]() =
=![]() ,与
,与![]() 联立可求出
联立可求出![]() 的值;
的值;
![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,如图
,如图![]() ,在
,在![]() 中利用勾股定理计算出
中利用勾股定理计算出![]() =
=![]() ,再利用面积法计算出
,再利用面积法计算出![]() ,接着在
,接着在![]() 中利用勾股定理计算出
中利用勾股定理计算出![]() ,则可得到
,则可得到![]() ,根据圆周角定理得到
,根据圆周角定理得到![]() =
=![]() ,于是得到
,于是得到![]() .
.
解:(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]()
∴![]() ;
;
(2)连接![]() ,如图
,如图![]() ,
,

∵![]() =
=![]() ,
,
∴![]() 是
是![]() 的直径,
的直径,
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() =
=![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
由于![]() ,则方程化为
,则方程化为![]() =
=![]() ,解得
,解得![]() =
=![]() ,
,![]() =
=![]() (舍去),
(舍去),
∴![]() 的值为
的值为![]() ;
;
(3)![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,如图
,如图![]() ,
,
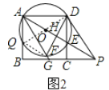
∵![]() =
=![]() ,
,
∴![]() 为
为![]() 的直径,
的直径,
在![]() 中,
中,
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴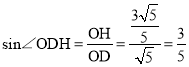 ,
,
∵![]() =
=![]() ,
,
∴![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③
;③![]() .其中正确的是( )
.其中正确的是( )
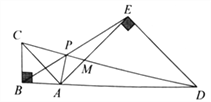
A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.

请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
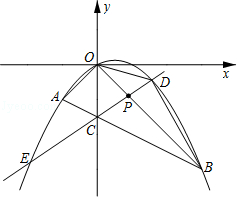
【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c–3b<0;⑤a+b>n(an+b)(n≠1),其中正确的结论有( )
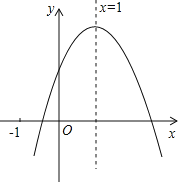
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]()

(1)求直线![]() 的解析式;
的解析式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),当
重合),当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:如果存在常数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ≤
≤![]() ,那么称这个函数是有上界函数;在所有满足条件的
,那么称这个函数是有上界函数;在所有满足条件的![]() 中,其最小值称为这个函数的上确界.例如,函数
中,其最小值称为这个函数的上确界.例如,函数![]() ,
, ![]() ≤2,因此是有上界函数,其上确界是2.如果函数
≤2,因此是有上界函数,其上确界是2.如果函数![]() (
(![]() ≤x≤
≤x≤![]() ,
, ![]() <
<![]() )的上确界是
)的上确界是![]() ,且这个函数的最小值不超过2
,且这个函数的最小值不超过2![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() ≤
≤![]() B.
B. ![]() C.
C. ![]() ≤
≤![]() D.
D. ![]() ≤
≤![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com