练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一次函数的图像与反比例函数(k＞0)的图像交于A，B两点，过点A做x轴的垂线，垂足为M，△AOM面积为1.

    （1）求反比例函数的解析式；

    （2）在y轴上求一点P,使PA+PB的值最小，并求出其最小值和P点坐标.

    【答案】（1）y=；（2）最小值即为，P（0，）.

    【解析】

    （1）根据反比例函数比例系数的几何意义得出，进而得到反比例函数的解析式；

    （2）作点关于轴的对称点，连接，交轴于点，得到最小时，点的位置，根据两点间的距离公式求出最小值的长；利用待定系数法求出直线的解析式，得到它与轴的交点，即点的坐标．

    （1）反比例函数的图象过点，过点作轴的垂线，垂足为，面积为1，

    ，

    ，

    ，

    故反比例函数的解析式为：；

    （2）作点关于轴的对称点，连接，交轴于点，则最小．

    由，解得，或，

    ，，

    ，最小值．

    设直线的解析式为，

    则，解得，

    直线的解析式为，

    时，，

    点坐标为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

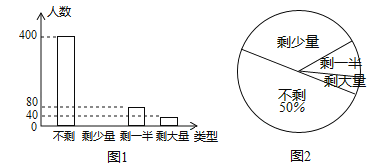
    【题目】某企业工会开展“一周工作量完成情况”调查活动，随机调查了部分员工一周的工作量剩余情况，并将调查结果统计后绘制成如图 1 和图 2 所示的不完整统计图 ．

    （1） 被调查员工的人数为　　人：

    （2） 把条形统计图补充完整；

    （3） 若该企业有员工 10000 人，请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

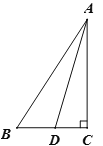
    【题目】如图，Rt△ ABC中，∠ACB=90°，AD平分∠BAC， 作AD的垂直平分线EF交AD于点E，交BC的延长线于点F，交AB于点G，交AC于点H．

    (1)依题意补全图形；

    (2)求证：∠BAD=∠BFG；

    (3)试猜想AB，FB和FD之间的数量关系并进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，Rt△中，，点为上一点，，，过点作的垂线交射线于点，延长交于点.

    （1）求的长；

    （2）求的正切值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加______m.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=mx+n与反比例函数y=其中m、n为常数，且mn＜0，则它们在同一坐标系中的图象可能是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.

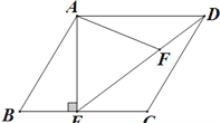
    (1)求证：∠DAF＝∠CDE；

    (2)求证：△ADF∽△DEC；

    (3)若AE＝6，AD＝8，AB＝7，求AF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

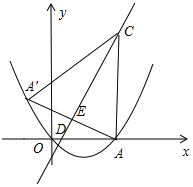
    【题目】如图所示，抛物线y=ax2-x+c经过原点O与点A（6，0）两点，过点A作AC⊥x轴，交直线y=2x-2于点C，且直线y=2x-2与x轴交于点D．

    （1）求抛物线的解析式，并求出点C和点D的坐标；

    （2）求点A关于直线y=2x-2的对称点A′的坐标，并判断点A′是否在抛物线上，并说明理由；

    （3）点P（x，y）是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点Q，设线段PQ的长为l，求l与x的函数关系式及l的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一平面直角坐标系中，反比例函数y（b≠0）与二次函数y＝ax2+bx（a≠0）的图象大致是（　　）

    A. B.

    C. D.

    查看答案和解析>>

    同步练习册答案