
 已知,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,∠ADB=60°,E、F、G分别是OA、OB、CD的中点,判断△EFG的形状,并说明理由.
已知,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,∠ADB=60°,E、F、G分别是OA、OB、CD的中点,判断△EFG的形状,并说明理由.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 证明:连接DE、CF,如图,
证明:连接DE、CF,如图,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图,C在直线BE上,∠ABC与∠ACE的角平分线交于点A1.
如图,C在直线BE上,∠ABC与∠ACE的角平分线交于点A1.查看答案和解析>>
科目:初中数学 来源: 题型:
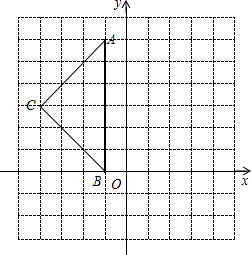 如图,在平面直角坐标系中,A(-1,6)、B(-1,0)、C(-4,3).
如图,在平面直角坐标系中,A(-1,6)、B(-1,0)、C(-4,3).查看答案和解析>>
科目:初中数学 来源: 题型:
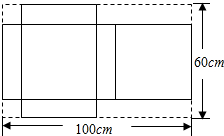 如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.
如图,有一块矩形铁皮,长100cm,宽60cm,在它的四角各切去两个同样的大小的正方形和两个同样大小的矩形剩下的铁皮正好做成一个带盖的长方体盒子,如果盒子的底面积为1600cm2,求该盒子的高.查看答案和解析>>
科目:初中数学 来源: 题型:
| p | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| n | 119 | 133 | 147 | 161 | 175 | 189 | 203 |
查看答案和解析>>
科目:初中数学 来源: 题型:
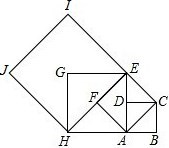 如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….
如图,四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去….查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com