
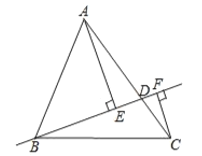
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点,分别过点
上任意一点,分别过点![]() 、
、![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() ,
,![]() ,
,![]() ,则
,则![]() 的最大值是______________,最小值是______________.
的最大值是______________,最小值是______________.
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】若抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于正半轴C点,且AC=20,BC=15,∠ACB=90°,则此抛物线的解析式为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
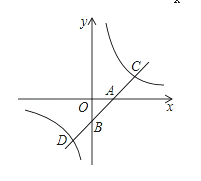
【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=![]() 于点C、D.
于点C、D.
(1)求k、b的值;
(2)写出不等式kx+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
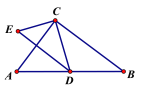
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC.
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
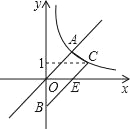
【题目】如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,﹣4),则四边形AOBC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
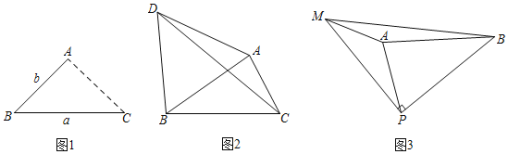
【题目】(1)发现:如图1,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]()
![]() ,当点
,当点![]() 位于 时,线段
位于 时,线段![]() 的长取得最大值,最大值为 (用含
的长取得最大值,最大值为 (用含![]() 的式子表示);
的式子表示);
(2)应用:如图2,点![]() 为线段
为线段![]() 外一动点,
外一动点,![]() ,
,![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,求线段
,求线段![]() 的最大值;
的最大值;
(3)拓展:如图3,线段![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 长的最大值及此时
长的最大值及此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
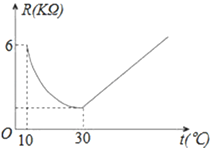
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻随温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求当10≤t≤30时,R和t之间的关系式;
(2)求温度在30℃时电阻R的值;并求出t≥30时,R和t之间的关系式;
(3)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过6 kΩ?
查看答案和解析>>
科目:初中数学 来源: 题型:
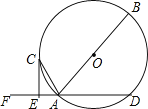
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
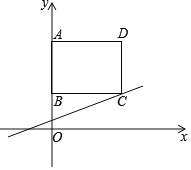
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、D的坐标分别为(0,5)、(0,2)、(4,5),直线l的解析式为y=kx+2﹣4k(k>0).
(1)当直线l经过原点O时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点C;
(3)在(1)的条件下,点M为直线l上的点,平面内是否存在x轴上方的点N,使以点O、A、M、N为顶点的四边形是菱形?若存在,请直接写出点M的坐标:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com