
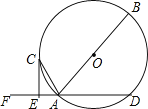
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
【答案】(1)证明见解析;(2)2.5.
【解析】
试题(1)证明:连接CO,证得∠OCA=∠CAE,由平行线的判定得到OC∥FD,再证得OC⊥CE,即可证得结论;
(2)证明:连接BC,由圆周角定理得到∠BCA=90°,再证得△ABC∽△ACE,根据相似三角形的性质即可证得结论.
试题解析:(1)证明:连接CO,∵OA=OC,∴∠OCA=∠OAC,∵AC平分∠FAB,∴∠OCA=∠CAE,∴OC∥FD,∵CE⊥DF,∴OC⊥CE,∴CE是⊙O的切线;
(2)证明:连接BC,在Rt△ACE中,AC=![]() =
=![]() =
=![]() ,∵AB是⊙O的直径,∴∠BCA=90°,∴∠BCA=∠CEA,∵∠CAE=∠CAB,∴△ABC∽△ACE,∴
,∵AB是⊙O的直径,∴∠BCA=90°,∴∠BCA=∠CEA,∵∠CAE=∠CAB,∴△ABC∽△ACE,∴![]() ,∴
,∴![]() ,∴AB=5,∴AO=2.5,即⊙O的半径为2.5.
,∴AB=5,∴AO=2.5,即⊙O的半径为2.5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
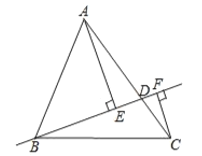
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点,分别过点
上任意一点,分别过点![]() 、
、![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() ,
,![]() ,
,![]() ,则
,则![]() 的最大值是______________,最小值是______________.
的最大值是______________,最小值是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
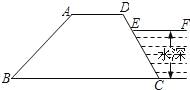
【题目】有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135°,∠ADC=120°,求水深.(精确到0.1米,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=﹣x+b分别与x轴,y轴交于A(6,0),B两点,过点B的另一直线交x轴的负半轴于点C,且OB:OC=3:1
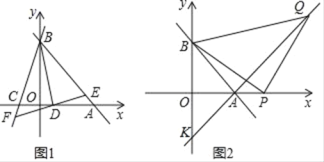
(1)求直线BC的解析式;
(2)直线y=ax﹣a(a≠0)交AB于点E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使S△BDE=S△BDF?若存在,求出a的值;若不存在,请说明理由;
(3)如图2,点P为A点右侧x轴上一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角三角形△BPQ,连接QA并延长交y轴于点K.当P点运动时,K点的位置是否发生变化?若不变,求出它的坐标;如果会发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的10×5网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点B按下列步骤移动第一步:点B绕点A逆时针旋转180°得到点B1;第二步:点B1绕点D逆时针旋转90°得到点B2;第三步:点B2绕点C逆时针旋转90°回到点B
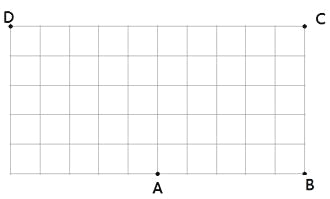
(1)请用圆规画出点B→B1→B2→B经过的路径;
(2)所画图形是_______图形;
(3)求所画图形的周长(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
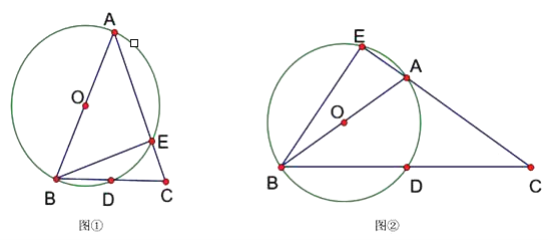
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜店第一次用400元购进某种蔬菜,由于销售状况良好,该店又用700元第二次购进该品种蔬菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有2% 的损耗,第二次购进的蔬菜有3% 的损耗,若该蔬菜店售完这些蔬菜获利不低于944元,则该蔬菜每千克售价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com