
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпyЃНЉx+bЗжБ№гыxжсЃЌyжсНЛгкAЃЈ6ЃЌ0ЃЉЃЌBСНЕуЃЌЙ§ЕуBЕФСэвЛжБЯпНЛxжсЕФИКАыжсгкЕуCЃЌЧвOBЃКOCЃН3ЃК1
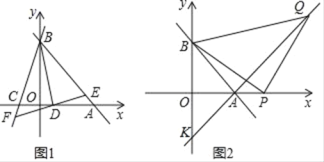
ЃЈ1ЃЉЧѓжБЯпBCЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпyЃНaxЉaЃЈaЁй0ЃЉНЛABгкЕуEЃЌНЛBCгкЕуFЃЌНЛxжсгкЕуDЃЌЪЧЗёДцдкетбљЕФжБЯпEFЃЌЪЙSЁїBDEЃНSЁїBDFЃПШєДцдкЃЌЧѓГіaЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуPЮЊAЕугвВрxжсЩЯвЛЖЏЕуЃЌвдPЮЊжБНЧЖЅЕуЃЌBPЮЊбќдкЕквЛЯѓЯоФкзїЕШбќжБНЧШ§НЧаЮЁїBPQЃЌСЌНгQAВЂбгГЄНЛyжсгкЕуKЃЎЕБPЕудЫЖЏЪБЃЌKЕуЕФЮЛжУЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓГіЫќЕФзјБъЃЛШчЙћЛсЗЂЩњБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН3x+6ЃЛЃЈ2ЃЉДцдкЃЌaЃН![]() ЃЛЃЈ3ЃЉKЕуЕФЮЛжУВЛЗЂЩњБфЛЏЃЌKЃЈ0ЃЌЉ6ЃЉ
ЃЛЃЈ3ЃЉKЕуЕФЮЛжУВЛЗЂЩњБфЛЏЃЌKЃЈ0ЃЌЉ6ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШШЗЖЈBЁЂCСНЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉгЩSЁїBDFЃНSЁїBDEПЩжЊжЛашDFЃНDEЃЌМДDЮЊEFжаЕуЃЌСЊСЂНтЮіЪНЧѓГіEЁЂFСНЕузјБъЃЌРћгУжаЕузјБъЙЋЪНСаГіЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЙ§ЕуQзїQCЁЭxжсЃЌжЄУїЁїBOPЁеЁїPCQЃЌЧѓГіACЃНQCЃЌМДПЩЭЦГіЁЯQACЃНЁЯOAKЃН45ЁуЃЌМДПЩНтОіЮЪЬт.
НтЃКЃЈ1ЃЉЁпжБЯпyЃНЉx+bгыxжсНЛгкAЃЈ6ЃЌ0ЃЉЃЌ
Ёр0ЃНЉ6+bЃЌНтЕУЃКbЃН6ЃЌ
ЁржБЯпABЕФНтЮіЪНЪЧЃКyЃНЉx+6ЃЌ
ЁрBЃЈ0ЃЌ6ЃЉЃЌ
ЁрOBЃН6ЃЌ
ЁпOBЃКOCЃН3ЃК1ЃЌ
ЁрOCЃН2ЃЌ
ЁрCЃЈЉ2ЃЌ0ЃЉ
ЩшжБЯпBCЕФНтЮіЪНЪЧyЃНkx+bЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФНтЮіЪНЪЧЃКyЃН3x+6ЃЛ
ЃЈ2ЃЉДцдкЃЎ
РэгЩЃК ЁпSЁїBDFЃНSЁїBDEЃЌ
ЁржЛашDFЃНDEЃЌМДDЮЊEFжаЕуЃЌ
ЁпЕуEЮЊжБЯпABгыEFЕФНЛЕуЃЌ
СЊСЂ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК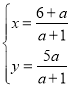 ЃЌ
ЃЌ
ЁрЕуEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЕуFЮЊжБЯпBCгыEFЕФНЛЕуЃЌ
СЊСЂ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК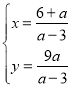 ЃЌ
ЃЌ
ЁрЕуFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпDЮЊEFжаЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрaЃН0ЃЈЩсШЅЃЉЃЌaЃН![]() ЃЌ
ЃЌ
ОМьбщЃЌaЃН![]() ЪЧдЗНГЬЕФНтЃЌ
ЪЧдЗНГЬЕФНтЃЌ
ЁрДцдкетбљЕФжБЯпEFЃЌaЕФжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉKЕуЕФЮЛжУВЛЗЂЩњБфЛЏЃЎ
РэгЩЃКШчЭМ2жаЃЌЙ§ЕуQзїQCЁЭxжсЃЌЩшPAЃНmЃЌ
ЁпЁЯPOBЃНЁЯPCQЃНЁЯBPQЃН90ЁуЃЌ
ЁрЁЯOPB+ЁЯQPCЃН90ЁуЃЌЁЯQPC+ЁЯPQCЃН90ЁуЃЌ
ЁрЁЯOPBЃНЁЯPQCЃЌ
ЁпPBЃНPQЃЌ
ЁрЁїBOPЁеЁїPCQЃЈAASЃЉЃЌ
ЁрBOЃНPCЃН6ЃЌOPЃНCQЃН6+mЃЌ
ЁрACЃНQCЃН6+mЃЌ
ЁрЁЯQACЃНЁЯOAKЃН45ЁуЃЌ
ЁрOAЃНOKЃН6ЃЌ
ЁрKЃЈ0ЃЌЉ6ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
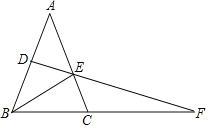
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЕуDЪЧABЕФжаЕуЃЌЕуFЪЧBCбгГЄЯпЩЯвЛЕуЃЌСЌНгDFЃЌНЛACгкЕуEЃЌСЌНгBEЃЌЁЯAЃНЁЯABE
ЃЈ1ЃЉЧѓжЄЃКEDЦНЗжЁЯAEBЃЛ
ЃЈ2ЃЉШєABЃНACЃЌЁЯAЃН38ЁуЃЌЧѓЁЯFЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
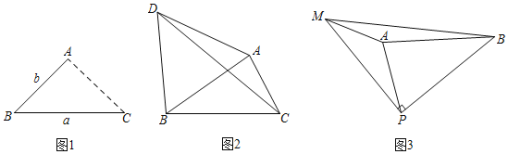
ЁОЬтФПЁПЃЈ1ЃЉЗЂЯжЃКШчЭМ1ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЭтвЛЖЏЕуЃЌЧв
ЭтвЛЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ![]()
![]() ЃЌЕБЕу
ЃЌЕБЕу![]() ЮЛгк ЪБЃЌЯпЖЮ
ЮЛгк ЪБЃЌЯпЖЮ![]() ЕФГЄШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ ЃЈгУКЌ
ЕФГЄШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ ЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉгІгУЃКШчЭМ2ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЭтвЛЖЏЕуЃЌ
ЭтвЛЖЏЕуЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвд
ЃЌвд![]() ЮЊБпзїЕШБп
ЮЊБпзїЕШБп![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЭиеЙЃКШчЭМ3ЃЌЯпЖЮ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЭтвЛЖЏЕуЃЌЧв
ЭтвЛЖЏЕуЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ГЄЕФзюДѓжЕМАДЫЪБ
ГЄЕФзюДѓжЕМАДЫЪБ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУХфЗНЗЈНтЯТСаЗНГЬЪБЃЌХфЗНгаДэЮѓЕФЪЧЃЈ ЃЉ
AЃЎx2Љ2xЉ99=0ЛЏЮЊЃЈxЉ1ЃЉ2=100
BЃЎx2+8x+9=0ЛЏЮЊЃЈx+4ЃЉ2=25
CЃЎ2t2Љ7tЉ4=0ЛЏЮЊЃЈtЉ![]() ЃЉ2=
ЃЉ2=![]()
DЃЎ3x2Љ4xЉ2=0ЛЏЮЊЃЈxЉ![]() ЃЉ2=
ЃЉ2=![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
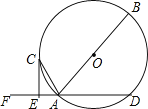
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌADЪЧЁбOЕФЯвЃЌЕуFЪЧDAбгГЄЯпЕФвЛЕуЃЌACЦНЗжЁЯFABНЛЁбOгкЕуCЃЌЙ§ЕуCзїCEЁЭDFЃЌДЙзуЮЊЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКCEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAE=1ЃЌCE=2ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
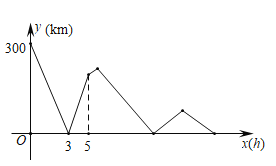
ЁОЬтФПЁПШчЭМЃЌвЛИіСЃзгдк![]() жсЩЯМАЕквЛЯѓЯоФкдЫЖЏЃЌЕк1ДЮДг
жсЩЯМАЕквЛЯѓЯоФкдЫЖЏЃЌЕк1ДЮДг![]() дЫЖЏЕН
дЫЖЏЕН![]() ЃЌЕк2ДЮДг
ЃЌЕк2ДЮДг![]() дЫЖЏЕН
дЫЖЏЕН![]() ЃЌЕк3ДЮДг
ЃЌЕк3ДЮДг![]() дЫЖЏЕН
дЫЖЏЕН![]() ЃЌЫќНгзХАДЭМжаМ§ЭЗЫљЪОЕФЗНЯђдЫЖЏЃЎдђЕк2019ДЮЪБдЫЖЏЕНДяЕФЕуЮЊЃЈ ЃЉ
ЃЌЫќНгзХАДЭМжаМ§ЭЗЫљЪОЕФЗНЯђдЫЖЏЃЎдђЕк2019ДЮЪБдЫЖЏЕНДяЕФЕуЮЊЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНГЕЗжБ№Дг![]() ЁЂ
ЁЂ![]() СНЕиЭЌЪБЯрЯђдШЫйааЪЛЃЌЕБввГЕЕНДя
СНЕиЭЌЪБЯрЯђдШЫйааЪЛЃЌЕБввГЕЕНДя![]() ЕиКѓЃЌМЬајБЃГждЫйЯђдЖРы
ЕиКѓЃЌМЬајБЃГждЫйЯђдЖРы![]() ЕФЗНЯђааЪЛЃЌЖјМзГЕЕНДя
ЕФЗНЯђааЪЛЃЌЖјМзГЕЕНДя![]() ЕиКѓЃЌанЯЂАыаЁЪБКѓСЂМДЕєЭЗЃЌВЂвддЫйЕФ
ЕиКѓЃЌанЯЂАыаЁЪБКѓСЂМДЕєЭЗЃЌВЂвддЫйЕФ![]() БЖгыввГЕЭЌЯђааЪЛЃЌОЙ§вЛЖЮЪБМфКѓЃЌСНГЕЯШКѓЕНДяОр
БЖгыввГЕЭЌЯђааЪЛЃЌОЙ§вЛЖЮЪБМфКѓЃЌСНГЕЯШКѓЕНДяОр![]() Еи
Еи![]() ЕФ
ЕФ![]() ЕиВЂЭЃЯТРДЃЌЩшСНГЕааЪЛЕФЪБМфЮЊ
ЕиВЂЭЃЯТРДЃЌЩшСНГЕааЪЛЕФЪБМфЮЊ![]() ЃЌСНГЕжЎМфЕФОрРыЮЊ
ЃЌСНГЕжЎМфЕФОрРыЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕШчЭМЃЌдђЕБМзГЕДг
ЕФКЏЪ§ЙиЯЕШчЭМЃЌдђЕБМзГЕДг![]() ЕиЕєЭЗзЗЕНввГЕЪБЃЌввГЕОрРы
ЕиЕєЭЗзЗЕНввГЕЪБЃЌввГЕОрРы![]() Еи__________
Еи__________![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
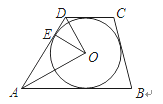
ЁОЬтФПЁПШчЭМЃЌдкЬнаЮABCDжаЃЌABЁЮCDЃЌЁбOЮЊФкЧадВЃЌEЮЊЧаЕуЃЎ
(1)ЧѓжЄЃКAO2=AEADЃЛ
(2)ШєAO=4cmЃЌAD=5cmЃЌЧѓЁбOЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
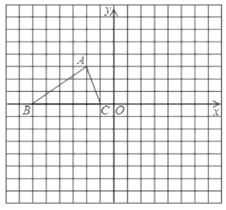
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ
ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЛГі![]() ЙигкдЕуЖдГЦЕФШ§НЧаЮ
ЙигкдЕуЖдГЦЕФШ§НЧаЮ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНЋШ§НЧаЮ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ШЦзјБъдЕу
ШЦзјБъдЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЛГіЭМаЮЃЌжБНгаДГі
ЃЌЛГіЭМаЮЃЌжБНгаДГі![]() ЕФЖдгІЕуЕФзјБъЃЎ
ЕФЖдгІЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com