
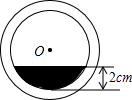
 将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )
将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是( )| A. | ($\frac{16}{3}$π-4$\sqrt{3}$)cm2 | B. | ($\frac{16}{3}$π-8$\sqrt{3}$)cm2 | C. | ($\frac{8}{3}$π-4$\sqrt{3}$)cm2 | D. | ($\frac{4}{3}$π-2$\sqrt{3}$)cm2 |
分析 作OD⊥AB于C,交小⊙O于D,则CD=2,由垂径定理可知AC=CB,利用正弦函数求得∠OAC=30°,进而求得∠AOC=120°,利用勾股定理即可求出AB的值,从而利用S扇形-S△AOB求得杯底有水部分的面积.
解答 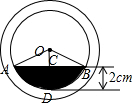 解:作OD⊥AB于C,交小⊙O于D,则CD=2,AC=BC,
解:作OD⊥AB于C,交小⊙O于D,则CD=2,AC=BC,
∵OA=OD=4,CD=2,
∴OC=2,
在RT△AOC中,sin∠OAC=$\frac{OC}{OA}$=$\frac{1}{2}$,
∴∠OAC=30°,
∴∠AOB=120°,
AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=2$\sqrt{3}$,
∴AB=4$\sqrt{3}$,
∴杯底有水部分的面积=S扇形-S△AOB=$\frac{120π×{4}^{2}}{360}$-$\frac{1}{2}$×$4\sqrt{3}$×2=($\frac{16}{3}$π-4$\sqrt{3}$)cm2
故选A.
点评 本题考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
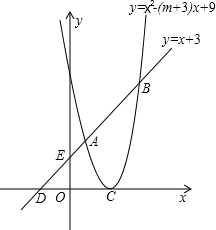 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴交于D、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
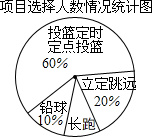 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
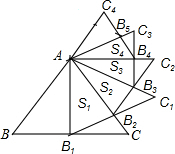 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这组数据的众数是170 | |
| B. | 这组数据的中位数是169 | |
| C. | 这组数据的平均数是169 | |
| D. | 若从8名学生中任选1名学生参加校文艺会演,则这名学生的身高不低于170的概率为$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com