练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点P（a，a）是反比例函数y= 在第一象限内的图象上的一个点，以点P为顶点作等边△PAB，使A、B落在x轴上，则△POA的面积是（　　）
    A.3
    B.4
    C.
    D.

    【答案】D
    【解析】解：如图，∵点P（a，a）是反比例函数y= 在第一象限内的图象上的一个点， ∴16=a2 ， 且a＞0，
    解得，a=4，
    ∴PD=4．
    ∵△PAB是等边三角形，
    ∴AD= = ．
    ∴OA=4﹣AD= ，
    ∴S△POA= OAPD= × ×4= ．
    故选D．

    【考点精析】通过灵活运用比例系数k的几何意义和等边三角形的性质，掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积；等边三角形的三个角都相等并且每个角都是60°即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知ΔABC的三边长为a、b、c，下列条件能够说明ΔABC是直角三角形的是（ ）

    A. a：b：c＝5：12：15 B. 3a=4b=5c C. a：b：c＝1：2： D. a=b=c

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（　　）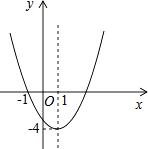
    A.图象关于直线x=1对称
    B.函数y=ax2+bx+c（a≠0）的最小值是﹣4
    C.﹣1和3是方程ax2+bx+c=0（a≠0）的两个根
    D.当x＜1时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们定义三个有理数之间的新运算法则“⊕”：a⊕b⊕c＝（|a﹣b﹣c|+a+b+c），如：1⊕（﹣2）⊕3＝ [|1﹣（﹣2）﹣3|+1+（﹣2）+3]＝l，在﹣2，﹣4，﹣5，0，2，5，6这7个数中，任意取三个数作为a，b，c的值，进行“a⊕b⊕c“运算，求在所有计算的结果中的最大值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上有A、B、C三个点对应的数分别是a、b、c，满足|a+24|+|b+10|+（c﹣10）2=0；动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A．在返回过程中，当t=_____秒时，P、Q两点之间的距离为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某游泳池有水4000m3 ， 先放水清洗池子．同时，工作人员记录放水的时间x（单位：分钟）与池内水量y（单位：m3） 的对应变化的情况，如下表：

    时间x（分钟）

    …

    10

    20

    30

    40

    …

    水量y（m3）

    …

    3750

    3500

    3250

    3000

    …


    （1）根据上表提供的信息，当放水到第80分钟时，池内有水多少m3？
    （2）请你用函数解析式表示y与x的关系，并写出自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（0，3），B（﹣3，5），C（﹣4，1）．

    ①把△ABC向右平移2个单位得△A1B1C1 ， 请画出△A1B1C1 ， 并写出点A1的坐标；
    ②把△ABC绕原点O旋转180°得到△A2B2C2 ， 请画出△A2B2C2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角梯形ABCD中，AB=2，BC=4，AD=6，M是CD的中点，点P在直角梯形的边上沿A→B→C→M运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示是（　　）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l：y= x+1交x轴于点A，交y轴于点B，点A1、A2、A3 ， …在x轴上，点B1、B2、B3 ， …在直线l上．若△OB1A1 ， △A1B2A2 ， △A2B3A3 ， …均为等边三角形，则△A5B6A6的周长是（　　）

    A.24
    B.48
    C.96
    D.192

    查看答案和解析>>

    同步练习册答案