
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,图2是由图1中阴影部分拼成的一个长方形,设图1中阴影部分面积为S1,图2中阴影部分面积为S2.
(1)请直接用含a,b的代数式表示S1=______,S2=_____;
(2)写出利用图形的面积关系所揭示的公式:_______;
(3)利用这个公式说明216﹣1既能被15整除,又能被17整除.

【答案】(1)a2﹣b2;(a+b)(a﹣b);(2)a2﹣b2=(a+b)(a﹣b);(3)证明见解析.
【解析】
(1)图1用大正方形的面积去掉小正方形的面积,图2用长方形的面积计算公式;
(2)因为两个图形的阴影部分面积相等,可以根据第(1)问列出等式;
(3)利用所得到的平方差公式分解因式后进行说明.
(1)图1用大正方形的边长为a,小正方形的边长为b,故阴影部分面积为a2﹣b2,图2用长方形的长为(a+b),宽为(a﹣b),故阴影部分面积为(a+b)(a﹣b);
(2)观察图1和图2中阴影部分面积是相等的,故a2﹣b2=(a+b)(a﹣b);
(3)216﹣1=(28﹣1)(28+1)=(24﹣1)(24+1)(28+1)=15×17×(28+1)
因为28+1是整数,故216﹣1既能被15整除,又能被17整除.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律: ①该蔬菜的销售价P(单位:元/千克)与时间x(单位:月份)满足关系:P=9﹣x
②该蔬菜的平均成本y(单位:元/千克)与时间x(单位:月份)满足二次函数关系y=ax2+bx+10,已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润L(单位:元/千克)最大?最大平均利润是多少?(注:平均利润=销售价﹣平均成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )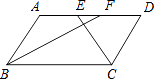
A.8
B.10
C.12
D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 . 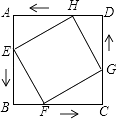
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系?请说明理由;


(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
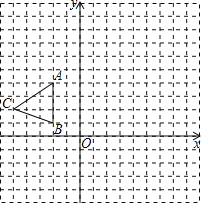
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)写出△A1B1C1的面积;△A2B2C2的面积.(不写解答过程,直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com