
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 设出原正方形的边长,按$\frac{1}{N}$在水平和垂直方向划两条线,可分出边长为$\frac{1}{N}$和$\frac{N-1}{N}$的两个正方形及长和宽为$\frac{1}{N}$和$\frac{N-1}{N}$的两个小长方形,而每个小正方形又可分为(N-1)个边长为$\frac{1}{N}$个边长为$\frac{1}{N}$的小正方形,故总的正方形数为2N,对于奇数(N≥7),同理可得出同样的结论.
解答 解:对任一正方形,容易分为大于等于4的偶数个小正方形(大小不等),比如2N,(N≥2).
具体分法为:设原正方形边长为1,按$\frac{1}{N}$在水平和垂直方向划两条线,这可分出边长为$\frac{1}{N}$和$\frac{N-1}{N}$两个正方形及长宽分别为$\frac{1}{N}$和$\frac{N-1}{N}$的两个小长方形,而每个小长方形又可分为(N-1)个边长为$\frac{1}{N}$的小正方形,因此总的正方形数为2+2×(N-1)=2N.
而对于奇数(N≥7),显然原正方形先可一分为四,而其中之一的小正方形又可分为大于等于4的偶数个小正方形(前一结论),计为2N,因此可分为3+2N=2(N+1)+1个奇数个小正方形,其中(N≥2),故N=4或N≥6的所有自然数.
故选A.
点评 本题考查了作图-应用与设计,作图主要把简单作图放入实际问题中,首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图,解题的关键是画出前几种图形,找到规律,再依此类推,这样比较直观.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
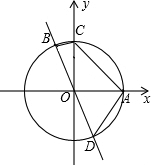 如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为4$\sqrt{2}$.
如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
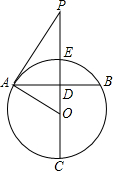 如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.
如图,过圆心O的直线PC垂直弦AB于点D,并且与⊙O交于C、E两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
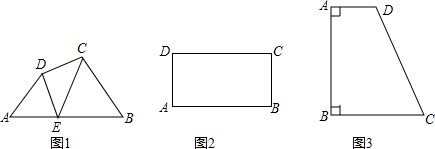
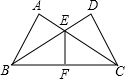 如图,∠A=∠D=90°,AB=DC,AC与BD相交于点E,F是BC的中点.下列说法:①BE=EC;②BF=FC;③EF⊥BC;④∠BEF=∠CEF,正确的有( )个.
如图,∠A=∠D=90°,AB=DC,AC与BD相交于点E,F是BC的中点.下列说法:①BE=EC;②BF=FC;③EF⊥BC;④∠BEF=∠CEF,正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com