
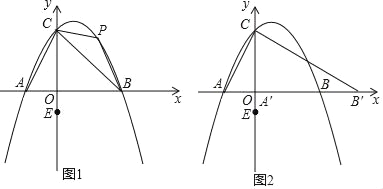
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+x+2
x2+x+2![]() 与x轴交于A、B两点,交y轴于点C,点C关于抛物线对称轴的对称点为点D.
与x轴交于A、B两点,交y轴于点C,点C关于抛物线对称轴的对称点为点D.
(1)求线段AC的长度;
(2)P为线段BC上方抛物线上的任意一点,点E为(0,﹣1),一动点Q从点P出发运动到y轴上的点G,再沿y轴运动到点E.当四边形ABPC的面积最大时,求PG+![]() GE的最小值;
GE的最小值;
(3)将线段AB沿x轴向右平移,设平移后的线段为A'B',直至A'P平行于y轴(点P为第2小问中符合题意的P点),连接直线CB'.将△AOC绕着O旋转,设旋转后A、C的对应点分别为A'、C',在旋转过程中直线A'C'与y轴交于点M,与线段CB'交于点N.当△CMN是以MN为腰的等腰三角形时,写出CM的长度.
【答案】(1)AC=![]() ;(2)PG+
;(2)PG+![]() GE的最小值为
GE的最小值为![]() ;(3)CM的长度为:2
;(3)CM的长度为:2![]() ﹣
﹣![]() 或
或![]() .
.
【解析】
(1)令y=0,则x=2![]() 或
或![]() ,令x=0,y=2
,令x=0,y=2![]() ,即:A(-
,即:A(-![]() ,0)、B(2
,0)、B(2![]() ,0)、C(0,2
,0)、C(0,2![]() ),则AC=
),则AC=![]() ;
;
(2)过点P作y轴的平行线交BC于点H,设:P的横坐标为m,则P(m,-![]() m2+m+2
m2+m+2![]() ),H(m,-m+2
),H(m,-m+2![]() ),S四边形ABPC=S△ABC+S△PBC,S△ABC是个常量,∴四边形ABPC的面积最大时,只需要确定S△PBC最大即可,求出此时P(
),S四边形ABPC=S△ABC+S△PBC,S△ABC是个常量,∴四边形ABPC的面积最大时,只需要确定S△PBC最大即可,求出此时P(![]() ,2
,2![]() ),过点E作RE⊥GR,使RE与y轴夹角为45度,则GR=
),过点E作RE⊥GR,使RE与y轴夹角为45度,则GR=![]() GE,则:PG+
GE,则:PG+![]() GE=PG+GR,当P、G、R三点共线时,PG+
GE=PG+GR,当P、G、R三点共线时,PG+![]() GE有最小值即可求解;
GE有最小值即可求解;
(3)分MN=CM、MN=CN两种情况求解即可.
(1)令y=0,则x=2![]() 或
或![]() ,令x=0,y=2
,令x=0,y=2![]() ,即:A(﹣
,即:A(﹣![]() ,0)、B(2
,0)、B(2![]() ,0)、C(0,2
,0)、C(0,2![]() ),
),
则AC=![]() ,BC所在的直线方程为:y=﹣x+2
,BC所在的直线方程为:y=﹣x+2![]() ;
;
(2)过点P作y轴的平行线交BC于点H,
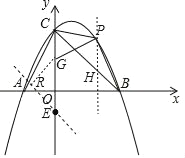
设:P的横坐标为m,则P(m,﹣![]() m2+m+2
m2+m+2![]() ),H(m,﹣m+2
),H(m,﹣m+2![]() ),
),
S四边形ABPC=S△ABC+S△PBC,S△ABC是个常量,∴四边形ABPC的面积最大时,只需要确定S△PBC最大即可,
S△PBC即=![]() PH(xB)=
PH(xB)=![]() (﹣
(﹣![]() m2+m+2
m2+m+2![]() +m﹣2
+m﹣2![]() )=
)=![]() (﹣
(﹣![]() m2+2m),
m2+2m),
当m=![]() 时,函数取得最大值,此时P(
时,函数取得最大值,此时P(![]() ,2
,2![]() ),
),
过点E作RE⊥GR,使RE与y轴夹角为45度,则GR=![]() GE,则:PG+
GE,则:PG+![]() GE=PG+GR,
GE=PG+GR,
当P、G、R三点共线时,PG+![]() GE有最小值,/span>
GE有最小值,/span>
直线ER的方程为y=﹣x﹣1…①,
则:直线PR方程的k值为1,其方程为:y=x+![]() …②,
…②,
联立①、②解得:R(﹣![]() ,
,![]() ),则:PR=
),则:PR=![]() ,
,
即PG+![]() GE的最小值为
GE的最小值为![]() ;
;
(3)①当MN=CM时,
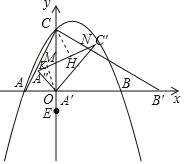
在等腰△MNC中,过C点作CH⊥MN,
设:MN=CM=a,CH=x,tan∠MCN=![]() =2,
=2,
由勾股定理得:a2=x2+(a﹣![]() )2,解得:x=
)2,解得:x=![]() a,
a,
则:tan∠CMH=![]() =
=![]() =tan∠A″MA′,
=tan∠A″MA′,
在△A″MA′中,A′M=CO﹣CM=2![]() ﹣a,A′A″=
﹣a,A′A″=![]() ,tan∠C′A″A′=2,
,tan∠C′A″A′=2,
过点O作A′K⊥A″C′,则:A′K=A′A″sinA″=![]() ,AM=
,AM=![]() ,
,
则:CM=2![]() ﹣
﹣![]() ;
;
②当MN=CN时,过点N作NS⊥CM,
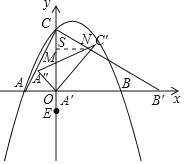
设N的横坐标为n,
∵tan∠MCN=![]() =2,∴CS=
=2,∴CS=![]() n,CM=n,
n,CM=n,
∵∠MA″A′=∠MCC′=∠CMC′=∠A′MA″,∴A′A″=A′M=2![]() ﹣n=
﹣n=![]() ,
,
∴CM=n=![]() ;
;
故:CM的长度为:2![]() ﹣
﹣![]() 或
或![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小明胜,否则,小军胜.
(1)请用树形图或列表法列出摸笔游戏所有可能的结果;
(2)请计算小明获胜的概率,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x+c经过A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)若点P在第一象限的抛物线上,且点P的横坐标为t,过点P向x轴作垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式,并求出m的最大值;
(3)在x轴上是否存在点E,使以点B,C,E为顶点的三角形为等腰三角形?如果存在,直接写出E点坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=![]() x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
(1)求该抛物线的函数表达式及顶点D的坐标;
(2)判断△ABC的形状,并求出△ABC的面积;
(3)将抛物线向左或向右平移,得到抛物线L′,L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com