
����Ŀ����֪������L��y��![]() x2+bx��2��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ������y���ཻ�ڵ�C���ҵ�A�������ǣ���1��0����
x2+bx��2��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ������y���ཻ�ڵ�C���ҵ�A�������ǣ���1��0����
��1����������ߵĺ�������ʽ������D�����ꣻ
��2���ж���ABC����״���������ABC�������
��3�������������������ƽ�ƣ��õ�������L�䣬L����x���ཻ��A'��B�����㣨��A���ڵ�B������ࣩ������y���ཻ�ڵ�C����Ҫʹ��A'B��C������ABC�������ȣ����������������������ߵĺ�������ʽ��

���𰸡�(1)y��![]() x2��
x2��![]() x��2������D��������
x��2������D��������![]() ����
����![]() ����(2)��ABC��ֱ�������Σ���ABC�������5��(3)�������������������ߵĺ�������ʽ��y��
����(2)��ABC��ֱ�������Σ���ABC�������5��(3)�������������������ߵĺ�������ʽ��y��![]() ��y��
��y��![]() ��y��
��y��![]() ��
��
��������
��1�����������߹���A������������ߵĽ���ʽ��Ȼ��������Ϊ����ʽ���ɵõ�����D�����ꣻ
��2�����ݣ�1���еĺ�������ʽ������õ�A��B��C�����꣬�Ӷ������ж���ABC����״��������������
��3������ƽ�Ƶ��ص�ͷ������۵ķ������������Ӧ�ĺ�������ʽ��
(1)��������L��y��![]() x2+bx��2����A����1��0����
x2+bx��2����A����1��0����
��0��![]() ������1��2+b������1����2��
������1��2+b������1����2��
��ã�b����![]() ��
��
��y��![]() x2��
x2��![]() x��2��
x��2��![]() ��
��
���D��������![]() ����
����![]() ����
����
���������ߵĺ�������ʽ��y��![]() x2��
x2��![]() x��2������D��������
x��2������D��������![]() ����
����![]() ����
����
(2)��y��0ʱ��0��![]() x2��
x2��![]() x��2����ã�x1����1��x2��4����x��0ʱ��y����2��
x��2����ã�x1����1��x2��4����x��0ʱ��y����2��
���A����1��0������B��4��0������C��0����2����
��AB��5��AC��![]() ��BC��2
��BC��2![]() ��
��
��AB2��AC2+BC2��
���ABC��ֱ�������Σ�
���ABC������ǣ�![]() ��5��
��5��
(3)�����������������ƽ�ƣ�
��ƽ�ƺ�A��B����ƽ��ǰ��AB�ij�����ȣ�
��ֻҪƽ�ƺ����0����2�������0��2��������������
������ƽ��ʱ��
��y��![]() ����x��0ʱ��y��
����x��0ʱ��y��![]() ��2����a��
��2����a��![]() ��
��
��ʱy��![]() ��
��![]() ��
��
������ƽ��ʱ��
��y��![]() ����x��0ʱ��y��
����x��0ʱ��y��![]() ����2����m��
����2����m��![]() ��m��3��
��m��3��
��m��![]() ʱ��y��
ʱ��y��![]() ����m��3ʱ��y��
����m��3ʱ��y��![]() ��2��
��2��
���Ͽɵã��������������������ߵĺ�������ʽ��y��![]() ��y��
��y��![]() ��y��
��y��![]() ��2��
��2��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
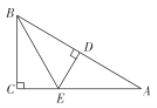
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() ����
����![]() �Ĵ�ֱƽ���ߣ���
�Ĵ�ֱƽ���ߣ���![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() ����
����![]() �� ��
�� ��
A.2B.1C.![]() D.3
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ö��ͨ�����������ӣ�����ö���ӵĵ�����ӣ�����һö���ӵĵ���Ϊ1���ڶ�ö���ӵĵ���Ϊ5����������Ϊ6����һ����������ǰ�˳�������1��5�������һ����Ϸ�涨��������Ϊ6��ʱ��Ӯ����������Ϊ9��ʱ�ҷ�Ӯ���������Ϸ________��������ƽ����������ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
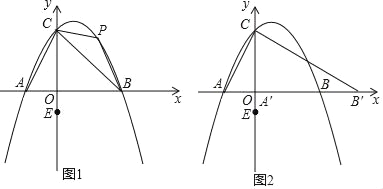
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����![]() x2+x+2
x2+x+2![]() ��x�ύ��A��B���㣬��y���ڵ�C����C���������߶Գ���ĶԳƵ�Ϊ��D��
��x�ύ��A��B���㣬��y���ڵ�C����C���������߶Գ���ĶԳƵ�Ϊ��D��
(1)���߶�AC�ij��ȣ�
(2)PΪ�߶�BC�Ϸ��������ϵ�����һ�㣬��EΪ��0����1����һ����Q�ӵ�P�����˶���y���ϵĵ�G������y���˶�����E�����ı���ABPC��������ʱ����PG+![]() GE����Сֵ��
GE����Сֵ��
(3)���߶�AB��x������ƽ�ƣ���ƽ�ƺ���߶�ΪA'B'��ֱ��A'Pƽ����y�ᣨ��PΪ��2С���з��������P�㣩������ֱ��CB'������AOC����O��ת������ת��A��C�Ķ�Ӧ��ֱ�ΪA'��C'������ת������ֱ��A'C'��y�ύ�ڵ�M�����߶�CB'���ڵ�N������CMN����MNΪ���ĵ���������ʱ��д��CM�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
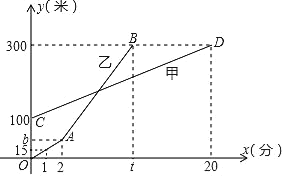
����Ŀ���ס���������Լ��ĩ�ǻ���ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺
��1����ɽ�������ٶ���ÿ������ ���ף�����A��ʱ�����ĸ߶�bΪ�� ���ף�
��2���������ٺ��ҵĵ�ɽ�����ٶ��Ǽ�ɽ�����ٶȵ�3����������ҵ�ɽȫ���У������ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ�����ϵʽ��
��3����ɽ�ʱ��ʱ���ס������˾����ĸ߶Ȳ�Ϊ70�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
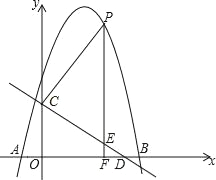
����Ŀ����ͼ��������y����x2+bx+c��x�ύ��A����1��0����B��5��0�����㣬ֱ��y����![]() x+3��y�ύ�ڵ�C����x�ύ�ڵ�D����P��ֱ��CD�Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
x+3��y�ύ�ڵ�C����x�ύ�ڵ�D����P��ֱ��CD�Ϸ�����������һ���㣬����P��PF��x���ڵ�F����ֱ��CD�ڵ�E�����P�ĺ�����Ϊm��
(1)�������ߵĽ���ʽ��
(2)��PE�ij����ʱm��ֵ��
(3)Q��ƽ��ֱ������ϵ��һ�㣬��(2)������£���PQCDΪ������ı�����ƽ���ı����Ƿ���ڣ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
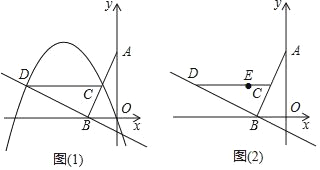
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬�߶�AB�������˵������ֱ�ΪA ��0��2����B����1��0������CΪ�߶�AB���е㣬�ֽ��߶�BA�Ƶ�B����ʱ�뷽����ת90��õ��߶�BD��������y��ax2+bx+c��a��0����������D��
(1)��ͼ1�����������߾���ԭ��O����a����1��
�����D�����꼰�������ߵĽ���ʽ��
������CD���ʣ������������Ƿ���ڵ�P��ʹ�á�POB���BCD���ࣿ�����ڣ�������������������ĵ�P�����꣬�������ڣ���˵�����ɣ�
(2)��ͼ2������������y��ax2+bx+c��a��0��������E����1��1������Q���������ϣ��������QOB���BCD���࣬������������Q��ĸ�����4������ֱ��д��a��ȡֵ��Χ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ݮ��ֲ�������ز�����������ժ����ݮ���ּӹ�����������ֱ���������ҵ��춼����������ֱ��������40Ԫ/�����ӹ�������130Ԫ/��(�������)����֪���ع�Ӷ20��������ÿ������ֻ�ܲ����ժ�ͼӹ��е�һ�����ÿ��ÿ����Բ�ժ70���ӹ�35�����谲��x�����˲�ժ��ݮ��ʣ�µĹ��˼ӹ���ݮ��
(1)������һ�������������ΪyԪ����y��x�ĺ�����ϵʽ��
(2)������η��乤��������ʹһ��������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
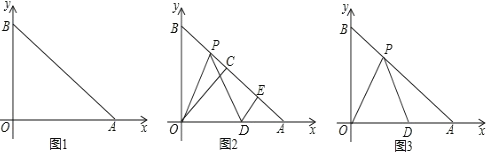
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ���߶�
���߶�![]() ��һ���㣬
��һ���㣬![]() ��
��![]() ����������һ�㣬��
����������һ�㣬��![]() ��
��![]() ��
��![]() ��
��
��1����![]() �Ķ�����
�Ķ�����
��2����ͼ2����![]() ������
������![]() �˶�ʱ��
�˶�ʱ��![]() ��ֵ�Ƿ�仯�����仯��˵�����ɣ������䣬����
��ֵ�Ƿ�仯�����仯��˵�����ɣ������䣬����![]() ��ֵ��
��ֵ��
��3����ͼ3����![]() ����
����![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com