
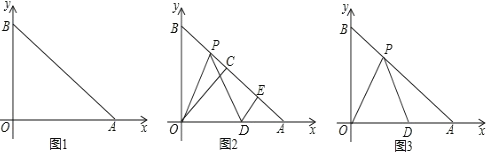
【题目】如图1在平面直角坐标系中,![]() 、
、![]() ,
,![]() 满足
满足![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一动点,
上一动点,![]() 是
是![]() 轴正半轴上一点,且
轴正半轴上一点,且![]() ,
,![]() 于
于![]() .
.
(1)求![]() 的度数;
的度数;
(2)如图2,设![]() ,当点
,当点![]() 运动时,
运动时,![]() 的值是否变化?若变化,说明理由;若不变,请求
的值是否变化?若变化,说明理由;若不变,请求![]() 的值;
的值;
(3)如图3,设![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)∠OAB=45°;(2)PE的值不变.理由见解析;(3)D(6![]() 6,0).
6,0).
【解析】
(1)根据非负数的性质即可求得a,b的值,从而得到△AOB是等腰直角三角形,据此即可求得;
(2)根据等腰三角形的性质以及三角形的外角的性质可以得到∠POC=∠DPE,即可证得△POC≌△DPE,则OC=PE,OC的长度根据等腰直角三角形的性质可以求得;
(3)利用等腰三角形的性质,以及外角的性质证得∠POC=∠DPE,即可证得△POC≌△DPE,根据全等三角形的对应边相等,即可求得OD的长,从而求得D的坐标.
(1)根据题意得:
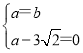 ,
,
解得:a=b=3![]() ,
,
∴OA=OB,
又∵∠AOB=90°
∴△AOB为等腰直角三角形,
∴∠OAB=45°.
(2)PE的值不变.理由如下:
∵△AOB为等腰直角三角形,且AC=BC,
∴∠AOC=∠BOC=45°
又∵OC⊥AB于C,
∵PO=PD
∴∠POD=∠PDO
当P在BC上时,
∵∠POD=45°+∠POC,∠PDO=45°+∠DPE,
∴∠POC=∠DPE
在△POC和△DPE中,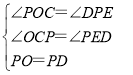 ,
,
∴△POC≌△DPE,
∴OC=PE
又OC=![]() AB=3
AB=3
∴PE=3;
当P在AC上时,∠POD=45°-∠POC,∠PDO=45°-∠DPE,
则∠POC=∠DPE.
同理可得PE=3;
(3)∵OP=PD,
∴∠POD=∠PDO=![]() =67.5°,
=67.5°,
则∠PDA=180°-∠PDO=180°-67.5°=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°-45°=22.5°,
∴∠BPO=180°-∠OPD-∠APD=112.5°,
∴∠PDA=∠BPO
则在△POB和△DPA中, ,
,
∴△POB≌△DPA(AAS).
∴PA=OB=3![]() ,
,
∴DA=PB=6-3![]() ,
,
∴OD=OA-DA=3![]() -(6-3
-(6-3![]() )=6
)=6![]() -6
-6
∴D(6![]() 6,0).
6,0).


科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=![]() x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
(1)求该抛物线的函数表达式及顶点D的坐标;
(2)判断△ABC的形状,并求出△ABC的面积;
(3)将抛物线向左或向右平移,得到抛物线L′,L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△ABC是格点三角形(三角形的三个顶点都是小正方形的顶点).
(1)在第一象限内找一点P,以格点P、A、B为顶点的三角形与△ABC相似但不全等,请写出符合条件格点P的坐标;
(2)请用直尺与圆规在第一象限内找到两个点M、N,使∠AMB=∠ANB=∠ACB.请保留作图痕迹,不要求写画法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
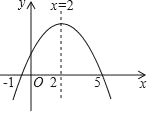
A. ac<0 B. a﹣b+c>0 C. b=﹣4a D. a+b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
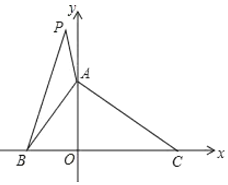
【题目】如图,已知在平面直角坐标系中,![]() 的面积为8,
的面积为8,![]() ,
,![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求![]() 三个顶点
三个顶点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)若点![]() 坐标为
坐标为![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(3)是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积?如果存在,请求出点
的面积?如果存在,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() .
.
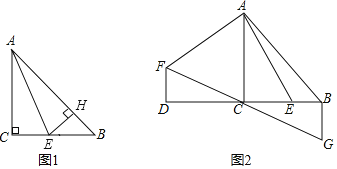
(1)如图1,当![]() 平分
平分![]() 时,
时,![]() 于
于![]() ,
,![]() 的周长为
的周长为![]() ,求
,求![]() 的长.
的长.
(2)如图2,延长![]() 至
至![]() ,使
,使![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90°得线段
顺时针旋转90°得线段![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
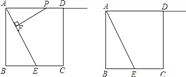
【题目】如图,正方形 ABCD 的边长为 4,E 是 BC 的中点,点 P 在射线 AD 上,过点 P 作 PF⊥AE,垂足为 F.
(1)求证:△PFA∽△ABE;
(2)当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶点的三角形也与△ABE
相似?若存在,求出 x 的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com