
【题目】某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
【答案】(1)y=-350x+63 000.(2)安排7名工人进行采摘,13名工人进行加工,才能使一天的收入最大,最大收入为60 550元.
【解析】试题(1)根据题意可知x人参加采摘蓝莓,则(20-x)人参加加工,可分别求出直接销售和加工销售的量,然后乘以单价得到收入钱数,列出函数的解析式;
(2)根据采摘量和加工量可求出x的取值范围,然后根据一次函数的增减性可得到分配方案,并且求出其最值.
试题解析:(1)根据题意得:![]() .
.
(2)因为![]() ,解得
,解得![]() ,又因为
,又因为![]() 为正整数,且
为正整数,且![]() .
.
所以![]() ,且
,且![]() 为正整数.
为正整数.
因为![]() ,所以
,所以![]() 的值随着
的值随着![]() 的值增大而减小,
的值增大而减小,
所以当![]() 时,
时,![]() 取最大值,最大值为
取最大值,最大值为![]() .
.
答:安排7名工人进行采摘,13名工人进行加工,才能使一天的收入最大,最大收入为60550元.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.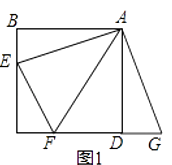
(1)【类比引申】如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;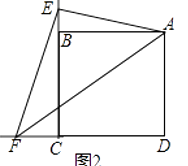
(2)【联想拓展】如图4,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下,![]() 不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得
不成立,但有些数可以使得它成立,例如:a=1,b=2.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)判断数对(﹣2,1),(3,3)是否是“相伴数对”;
(2)若(k,﹣1)是“相伴数对”,求k的值;
(3)若(4,m)是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
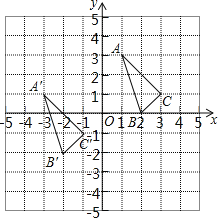
(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.
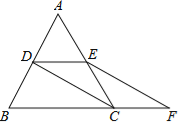
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明和小颖相约到乐山大佛景区参观.小明乘私家车从成都出发1小时后,小颖乘坐高铁从成都出发,先到乐山高铁站,然后转乘出租车到乐山大佛景区(换车时间忽略不计),两人恰好同时到达景区.他们离开成都的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.
(1)高铁的平均速度是每小时多少千米?
(2)当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A1B1C1;
(2)在直线l上找出一点P,使得|PA﹣PC|的值最大;(保留作图痕迹并标上字母P)
(3)在直线l上找出一点Q,使得QA+QC1的值最小;(保留作图痕迹并标上字母Q)
(4)在正方形网格中存在 个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校要建一个面积是81平方米的草坪,草坪周围用铁栅栏围绕,现有两种方案:有人建议建成正方形,也有人建议建成圆形,如果从节省铁栅栏费用的角度考虑(栅栏周长越小,费用越少),你选择哪种方案?请说明理由.(π取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m< ![]() ;④n≤1.
;④n≤1.
则所有正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com