
已知函数y=ax2+bx+c,当y>0时,﹣
 <x<
<x<
 .则函数y=cx2﹣bx+a的图象可能是图中的( )
.则函数y=cx2﹣bx+a的图象可能是图中的( )
A.
 B.
B.

C.
 D.
D.

B【考点】二次函数的图象.
【分析】当y>0时,﹣
 <x<
<x<
 ,所以可判断a<0,函数y=ax2+bx+c与x轴的交点为(﹣
,所以可判断a<0,函数y=ax2+bx+c与x轴的交点为(﹣
 ,0)和(
,0)和(
 ,0),即可求得﹣
,0),即可求得﹣
 =﹣
=﹣
 ,
,
 =﹣
=﹣
 ,得出a=6b,a=﹣6c,则b=﹣c,不妨设c=1,进而得出解析式,找出符合要求的答案.
,得出a=6b,a=﹣6c,则b=﹣c,不妨设c=1,进而得出解析式,找出符合要求的答案.
【解答】解:∵函数y=ax2+bx+c,当y>0时,﹣
 <x<
<x<
 .
.
∴a<0,c>0,函数y=ax2+bx+c与x轴的交点为(﹣
 ,0)和(
,0)和(
 ,0),
,0),
∴﹣
 =﹣
=﹣
 +
+
 =﹣
=﹣
 ,
,
 =﹣
=﹣
 ×
×
 =﹣
=﹣
 ,
,
∴a=6b,a=﹣6c,
∴b=﹣c,不妨设c=1
∴函数y=cx2﹣bx+a为函数y=x2+x﹣6
即y=(x﹣2)(x+3)
∴与x轴的交点坐标是(2,0),(﹣3,0).
故选B.
【点评】本题考查了二次函数的图象,根与系数的关系,根据二次函数与不等式的关系判断出a、b、c的正负情况以及a、c的关系是解题的关键.


科目:初中数学 来源: 题型:
如图,已知二次函数y=﹣
 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
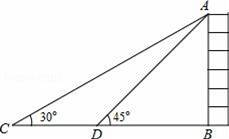
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: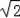
 ≈1.414,
≈1.414,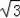
 ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
打市内电话都按时收费,并于200l年3月21日起对收费办法作了调整,调整前的收费办法:以3分钟为计时单位(不足3分钟按3分钟计),每个计时单位收0.2元;调整后的收费办法:3分钟内(含3分钟)0.2元,以后每加1分钟加收0.1元.
(1)根据调整后的收费办法,求电话费y(元)与通话时间t(分)之间的函数关系式(t>3时设t(分)表示正整数).
①当t 3时,y= ;
3时,y= ;
②当t>3时(t(分)表示正整数),y=  .
.
(2)对(1),试画出0<t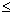 6时函数的图象.
6时函数的图象.
 (3)就0<t
(3)就0<t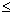 6,求t为何值时,调整前和调整后的电话费相同,并求出其相应的收费y(元).
6,求t为何值时,调整前和调整后的电话费相同,并求出其相应的收费y(元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com